Povrch tělesa - střední škola - příklady a úlohy
Počet nalezených příkladů: 246
- Povrch 32
 Povrch rotačního kužele a obsah jeho podstavy jsou v poměru 18:5. Určete objem kužele, je-li jeho tělesná výška 12 cm.
Povrch rotačního kužele a obsah jeho podstavy jsou v poměru 18:5. Určete objem kužele, je-li jeho tělesná výška 12 cm. - Prosím 6
 Prosím o vyjádření r ze vzorce pro povrch válce.
Prosím o vyjádření r ze vzorce pro povrch válce. - Průmer válce
 Povrch válce je 149 cm². Vyška válce je 6 cm. Kolik je průmer válce?
Povrch válce je 149 cm². Vyška válce je 6 cm. Kolik je průmer válce? - Objem z povrchu
 Jaký je objem krychle, jejíž povrch je 96 cm²?
Jaký je objem krychle, jejíž povrch je 96 cm²? - Krychle
 Krychli o hraně 1 m je opsána koule (vrcholy krychle leží na povrchu koule). Určete velikost povrchu teto koule.
Krychli o hraně 1 m je opsána koule (vrcholy krychle leží na povrchu koule). Určete velikost povrchu teto koule. - Povrch válce
 Vypočtěte povrch válce, je-li jeho objem 45 litrů a obvod podstavy je trojnásobkem výšky.
Vypočtěte povrch válce, je-li jeho objem 45 litrů a obvod podstavy je trojnásobkem výšky. - Čtverečních 4588
 Jaký je objem koule, jejíž povrch je 113,04m čtverečních?
Jaký je objem koule, jejíž povrch je 113,04m čtverečních? - Krychle
 Objemy dvou krychlí jsou v poměru 27:8. V jakém poměru jsou povrchy těchto krychlí?
Objemy dvou krychlí jsou v poměru 27:8. V jakém poměru jsou povrchy těchto krychlí? - Baňka chemická
 Vyfouknutá baňka tvaru koule má objem 0,6 litrů. Jaký má povrch?
Vyfouknutá baňka tvaru koule má objem 0,6 litrů. Jaký má povrch? - Poloměr 6
 Poloměr koule zmenšíme o 1/3 původního poloměru. O kolik procent se změní objem a povrch koule?
Poloměr koule zmenšíme o 1/3 původního poloměru. O kolik procent se změní objem a povrch koule? - Povrch válce
 Průměr podstavy válce je třetina délky výšky válce. Vypočtěte povrch, je-li objem 2m³.
Průměr podstavy válce je třetina délky výšky válce. Vypočtěte povrch, je-li objem 2m³. - Kužel těžký
 Povrch kužele je 200 cm², jeho výška je 7 centimetrů. Spočítej objem tohoto kužele.
Povrch kužele je 200 cm², jeho výška je 7 centimetrů. Spočítej objem tohoto kužele. - Celočíselných 7912
 Kolik existuje kvádrů o celočíselných rozměrech hran, pokud povrch je 48 m²?
Kolik existuje kvádrů o celočíselných rozměrech hran, pokud povrch je 48 m²? - Kolik
 Kolik m² desek 10mm hrubých třeba na zhotovení 12 bedýnek na květiny? Rozměry bedničky jsou 180,150 a 1500 mm.
Kolik m² desek 10mm hrubých třeba na zhotovení 12 bedýnek na květiny? Rozměry bedničky jsou 180,150 a 1500 mm. - Vypočítejte 38701
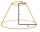 Vypočítejte povrch a objem seříznutého rotačního kužele s poloměry podstav 14cm a 8cm, výškou 11cm.
Vypočítejte povrch a objem seříznutého rotačního kužele s poloměry podstav 14cm a 8cm, výškou 11cm. - Válec obsah pláště
 Válec má obsah pláště 300 cm čtverečních, přičemž výška válce je 12 cm. Vypočítejte objem tohoto válce.
Válec má obsah pláště 300 cm čtverečních, přičemž výška válce je 12 cm. Vypočítejte objem tohoto válce. - Koule 20
 Koule má poloměr 2m. O kolik procent má větší povrch a objem jiná koule, jejíž poloměr je větší o 20%?
Koule má poloměr 2m. O kolik procent má větší povrch a objem jiná koule, jejíž poloměr je větší o 20%? - Řez kužele
 Objem kužele je 1000 cm³ a obsah jeho řezu je 100 cm². Vypočtěte povrch kužele.
Objem kužele je 1000 cm³ a obsah jeho řezu je 100 cm². Vypočtěte povrch kužele. - Okapové žlaby
 Urči spotřebu plechu na zhotovení žlabu, je-li třeba na spoje přidat 7 % materiálu. Délka žlabu je 2 m, průměr žlabu je 0,4 m.
Urči spotřebu plechu na zhotovení žlabu, je-li třeba na spoje přidat 7 % materiálu. Délka žlabu je 2 m, průměr žlabu je 0,4 m. - Krychle
 Povrchy kostek, z nichž jedna má hranu o 26 cm kratší než druhá, se liší o 18408 m². Určitě délky hran obou kostek.
Povrchy kostek, z nichž jedna má hranu o 26 cm kratší než druhá, se liší o 18408 m². Určitě délky hran obou kostek.
Máš úkol, nad kterým si lámeš alespoň 10 minut hlavu? Pošli nám úkol a my Ti ji zkusíme vypočítat.
