Příklady na obsah 17 - strana 2 z 23
Počet nalezených příkladů: 457
- Vzdálenost 145
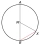 Vzdálenost tětivy od středu je 6 cm. Středový úhel je 60°. Vypočítejte plošný obsah kruhové úseče.
Vzdálenost tětivy od středu je 6 cm. Středový úhel je 60°. Vypočítejte plošný obsah kruhové úseče. - Kruh - úseč
 Kruh o průměru 30 cm je přeťat tětivou t = 16 cm. Vypočtěte obvod a obsah menší úseče.
Kruh o průměru 30 cm je přeťat tětivou t = 16 cm. Vypočtěte obvod a obsah menší úseče. - Jeden hektár
 Kolik má hektar metrů čtverečních?
Kolik má hektar metrů čtverečních? - Čtvereční 7482
 1dm čtvereční - 7000mm čtvereční
1dm čtvereční - 7000mm čtvereční
- Kolikrát 12001
 Kolikrát je 5 dm² méně než 100 m2
Kolikrát je 5 dm² méně než 100 m2 - Obraz na plánu
 Čtvercová zahrada má výměru 36m čtverečních. Jaký obsah bude mít její obraz na plánu v měřítku 1:60?
Čtvercová zahrada má výměru 36m čtverečních. Jaký obsah bude mít její obraz na plánu v měřítku 1:60? - Jak velkou
 Jak velkou tlakovou silou působí bagr na cestu, je-li obsah jeho pásů 5 m² a vznikne-li tlak 40 kPa?
Jak velkou tlakovou silou působí bagr na cestu, je-li obsah jeho pásů 5 m² a vznikne-li tlak 40 kPa? - Převod
 Vypočti a převeď: 0,2m² + 80dm² + 200cm² = kolik m2
Vypočti a převeď: 0,2m² + 80dm² + 200cm² = kolik m2 - Skutečnosti 79204
 V mapě měřítka 1:50 000 je zakresleno jezero o ploše 3 cm². Určete velikost jezera ve skutečnosti.
V mapě měřítka 1:50 000 je zakresleno jezero o ploše 3 cm². Určete velikost jezera ve skutečnosti.
- Hmotnost 5
 Hmotnost žáka a židle je 52 kg. Obsah dotykových ploch židle s podlahou je 12 centimetrů čtverečních. Jaký tlak způsobuje židle na podlahu?
Hmotnost žáka a židle je 52 kg. Obsah dotykových ploch židle s podlahou je 12 centimetrů čtverečních. Jaký tlak způsobuje židle na podlahu? - Tlak tanku
 Hmotnost tanku je 36 t, celková styková plocha pásů se zemí jsou 4 metry čtvereční. Jaký tlak způsobuje tank na vodorovnou plochu?
Hmotnost tanku je 36 t, celková styková plocha pásů se zemí jsou 4 metry čtvereční. Jaký tlak způsobuje tank na vodorovnou plochu? - Zahrádkáři
 Zahrádkáři platí městu za pronájem 1 m² pozemku 3 Kč. Kolik zaplatí ročně? a) 2 hektary b) 2 ary 150 m²
Zahrádkáři platí městu za pronájem 1 m² pozemku 3 Kč. Kolik zaplatí ročně? a) 2 hektary b) 2 ary 150 m² - Skutečnosti 5461
 Jakou plochu ve skutečnosti v arech znázorňuje 1 cm² na mapě o měřítku 1:20000?
Jakou plochu ve skutečnosti v arech znázorňuje 1 cm² na mapě o měřítku 1:20000? - Velký píst
 Velký píst hydraulického zařízení má obsah 0,25m² a malý 10 cm². Jak velkou silou musíme působit na malý píst, aby byl velký zvedán silou 750 N?
Velký píst hydraulického zařízení má obsah 0,25m² a malý 10 cm². Jak velkou silou musíme působit na malý píst, aby byl velký zvedán silou 750 N?
- Traktor 9
 Urči tlak vyvolaný pásovým traktorem o hmotnosti 30 t stojícím na vodorovné cestě, je-li obsah stykové plochy pásů se zemí 6 m čtverečních.
Urči tlak vyvolaný pásovým traktorem o hmotnosti 30 t stojícím na vodorovné cestě, je-li obsah stykové plochy pásů se zemí 6 m čtverečních. - Víno červené
 Víno červené polosladke s objemem 0,75L má obsah cukru: 18-45g/dm³. CKolik je to v přepočtu na kostky cukru?
Víno červené polosladke s objemem 0,75L má obsah cukru: 18-45g/dm³. CKolik je to v přepočtu na kostky cukru? - Hydraulický 3
 Hydraulický lis má písty o obsahu 20 cm² a 800 cm². Jak velká síla působí na větší píst, působíme-li na menší píst silou 100 N?
Hydraulický lis má písty o obsahu 20 cm² a 800 cm². Jak velká síla působí na větší píst, působíme-li na menší píst silou 100 N? - Traktoristé
 Traktoristé orali pole o rozloze 15 3/4 ha. Dopoledne zorali 3 1/3 ha, odpoledne 2 5/6 ha a v noci 4 1/4 ha. Kolik hektaru zbylo zorat a druhý den?
Traktoristé orali pole o rozloze 15 3/4 ha. Dopoledne zorali 3 1/3 ha, odpoledne 2 5/6 ha a v noci 4 1/4 ha. Kolik hektaru zbylo zorat a druhý den? - Obsah vody ve dřeve
 Dřevo obsahuje 12% vody. 1 m³ dřeva má hmotnost 650 kg. Kolik litrů vody obsahuje?
Dřevo obsahuje 12% vody. 1 m³ dřeva má hmotnost 650 kg. Kolik litrů vody obsahuje?
Máš úkol, nad kterým si lámeš alespoň 10 minut hlavu? Pošli nám úkol a my Ti ji zkusíme vypočítat.
