Pythagorova věta + procenta - příklady a úlohy - strana 2 z 5
Počet nalezených příkladů: 83
- Trojúhelníku 83152
 Daný je rovnoramenný trojúhelník, jehož základna je 8cm a ramena mají délku 15 cm. Vypočítej obsah trojúhelníku a poloměr vepsané a opsané kružnice.
Daný je rovnoramenný trojúhelník, jehož základna je 8cm a ramena mají délku 15 cm. Vypočítej obsah trojúhelníku a poloměr vepsané a opsané kružnice. - Trojúhelník 82416
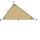 Jaké strany má pravoúhlý trojúhelník s obvodem 45 centimetrů as obsahem 67,5 cm²?
Jaké strany má pravoúhlý trojúhelník s obvodem 45 centimetrů as obsahem 67,5 cm²? - Trojúhelníku 73574
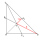 Dvě těžnice trojúhelníku jsou na sebe kolmé a mají 27 cm a 36 cm. Vypočítejte délku stran trojúhelníku a délku třetí těžnice.
Dvě těžnice trojúhelníku jsou na sebe kolmé a mají 27 cm a 36 cm. Vypočítejte délku stran trojúhelníku a délku třetí těžnice. - Šestiúhelníku 62524
 Podlaha v hrané věži má tvar pravidelného šestiúhelníku o délce strany 5m. Kolik kusů parket je třeba objednat na její pokrytí pokud na 1m čtverečních je zapotřebí 25 ks a je třeba připočítat rezervu 10%?
Podlaha v hrané věži má tvar pravidelného šestiúhelníku o délce strany 5m. Kolik kusů parket je třeba objednat na její pokrytí pokud na 1m čtverečních je zapotřebí 25 ks a je třeba připočítat rezervu 10%? - Horní a Dolní Ves
 Vzdálenost vzdušnou čarou mezi Dolní a Horní Vsí je 3 km a rovnoměrné stoupání je 5%. Jaký je výškový rozdíl mezi Horní a Dolní Vsí zaokrouhlený na celé metry?
Vzdálenost vzdušnou čarou mezi Dolní a Horní Vsí je 3 km a rovnoměrné stoupání je 5%. Jaký je výškový rozdíl mezi Horní a Dolní Vsí zaokrouhlený na celé metry? - Trojúhelníku 81666
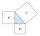 V pravoúhlém trojúhelníku, pokud a =x+34 a b = x a c= 50, pak vyřešte x. Strana c je přepona. Potom diskutujte o případě, kdy a nebo b je přepona.
V pravoúhlém trojúhelníku, pokud a =x+34 a b = x a c= 50, pak vyřešte x. Strana c je přepona. Potom diskutujte o případě, kdy a nebo b je přepona. - Trojúhelníku 81759
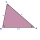 V trojúhelníku ABC známe a = 4 cm, b = 6 cm, γ = 60°. Vypočítejte obsah, poloměr vepsané a opsané kružnice.
V trojúhelníku ABC známe a = 4 cm, b = 6 cm, γ = 60°. Vypočítejte obsah, poloměr vepsané a opsané kružnice. - Zaokrouhlete 75064
 Vzhledem k trojúhelníku ABC, pokud strana b je 31 stop, strana c je 22 stop a úhel A je 47°, najděte stranu a. Zaokrouhlete na jedno desetinné místo.
Vzhledem k trojúhelníku ABC, pokud strana b je 31 stop, strana c je 22 stop a úhel A je 47°, najděte stranu a. Zaokrouhlete na jedno desetinné místo. - Rovnoběžníku 64414
 Rovnoběžník má stranu a = 58cm a úhlopříčky u=89cm, v = 52cm. Vypočítejte obvod a obsah tohoto rovnoběžníku.
Rovnoběžník má stranu a = 58cm a úhlopříčky u=89cm, v = 52cm. Vypočítejte obvod a obsah tohoto rovnoběžníku. - Trojúhelníku 67174
 Vypočítej odvěsnu s v pravoúhlém trojúhelníku STU ( pravý úhel při vrcholu U), je-li přepona dlouhá u=93cm a odvěsna t=48 cm
Vypočítej odvěsnu s v pravoúhlém trojúhelníku STU ( pravý úhel při vrcholu U), je-li přepona dlouhá u=93cm a odvěsna t=48 cm - Trojúhelník KLB
 Je dán rovnostranný trojúhelník ABC. Z bodu L který je středem strany BC tohoto trojúhelníku, je spuštěna kolmice k na stranu AB. Průsečík kolmice k a strany AB je označen jako bod K. Kolik % z obsahu trojúhelníku ABC tvoří trojúhelník KLB?
Je dán rovnostranný trojúhelník ABC. Z bodu L který je středem strany BC tohoto trojúhelníku, je spuštěna kolmice k na stranu AB. Průsečík kolmice k a strany AB je označen jako bod K. Kolik % z obsahu trojúhelníku ABC tvoří trojúhelník KLB? - Obvod a odvěsny
 Určete obvod pravoúhlého trojúhelníku, jestliže délka jedné odvěsny je 75% délky druhé odvěsny a jeho obsah je 24 cm².
Určete obvod pravoúhlého trojúhelníku, jestliže délka jedné odvěsny je 75% délky druhé odvěsny a jeho obsah je 24 cm². - Trojúhelníku 1910
 Najděte obsah trojúhelníku s danými rozměry. V případě potřeby zaokrouhlete roztok na nejbližší setinu. A = 50°, b = 30 stop, c = 14 stop
Najděte obsah trojúhelníku s danými rozměry. V případě potřeby zaokrouhlete roztok na nejbližší setinu. A = 50°, b = 30 stop, c = 14 stop - Trojúhelníku 72524
 Známe v pravoúhlém trojúhelníku výšku na přeponu vc = 4cm a přeponu c= 19cm. Jak vypočítat části strany - úseky na přeponě c1, c2
Známe v pravoúhlém trojúhelníku výšku na přeponu vc = 4cm a přeponu c= 19cm. Jak vypočítat části strany - úseky na přeponě c1, c2 - Kosinusova
 Kosinusova a sinusova věta : Vypočítejte všechny chybějící hodnoty z trojúhelníku ABC. a = 20 cm; b = 15 cm; γ = 90°; c =? cm; α =? °; β =? °
Kosinusova a sinusova věta : Vypočítejte všechny chybějící hodnoty z trojúhelníku ABC. a = 20 cm; b = 15 cm; γ = 90°; c =? cm; α =? °; β =? ° - Drak
 Janko má draka, který je tvaru kosočtverce. Jeho úhlopříčky jsou dlouhé 60 cm a 90 cm. Vypočítejte: a) stranu kosočtverce b) kolik papíru potřebuje Janko na draka, pokud jej potřebuje oblepit z obou stran a na zahnutí potřebuje 5% z celkové plochy papíru.
Janko má draka, který je tvaru kosočtverce. Jeho úhlopříčky jsou dlouhé 60 cm a 90 cm. Vypočítejte: a) stranu kosočtverce b) kolik papíru potřebuje Janko na draka, pokud jej potřebuje oblepit z obou stran a na zahnutí potřebuje 5% z celkové plochy papíru. - Trojúhelníku 70824
 Jedna odvěsna pravoúhlého trojúhelníku ABC má délku a= 14 cm a poloměr kružnice vepsané do tohoto trojúhelníku r= 5 cm. Vypočítejte délku přepony a jeho druhé odvěsny.
Jedna odvěsna pravoúhlého trojúhelníku ABC má délku a= 14 cm a poloměr kružnice vepsané do tohoto trojúhelníku r= 5 cm. Vypočítejte délku přepony a jeho druhé odvěsny. - Trojúhelníku 82696
 V trojúhelníku ABC je dáno b=5 cm, c=6 cm, /BAC/ = 80°. Vypočítejte velikosti ostatních stran a úhlů, dále určete velikosti těžnice tc a obsah trojúhelníku.
V trojúhelníku ABC je dáno b=5 cm, c=6 cm, /BAC/ = 80°. Vypočítejte velikosti ostatních stran a úhlů, dále určete velikosti těžnice tc a obsah trojúhelníku. - Obdélník
 V obdélníku se stranami 3 a 9 vyznačíme úhlopříčku. Jaká je pravděpodobnost, že náhodně zvolený bod uvnitř obdélníku je blíže k této úhlopříčce, jako k libovolné straně obdélníku?
V obdélníku se stranami 3 a 9 vyznačíme úhlopříčku. Jaká je pravděpodobnost, že náhodně zvolený bod uvnitř obdélníku je blíže k této úhlopříčce, jako k libovolné straně obdélníku? - Skelná mozaika
 Kolik dm² skla třeba na výrobu 39 sklíček tvaru pravidelného 6-úhelníku, jehož strana má délku 23 cm? Počítejte že při řezání skla vzniká odpad 12%.
Kolik dm² skla třeba na výrobu 39 sklíček tvaru pravidelného 6-úhelníku, jehož strana má délku 23 cm? Počítejte že při řezání skla vzniká odpad 12%.
Máš úkol, nad kterým si lámeš alespoň 10 minut hlavu? Pošli nám úkol a my Ti ji zkusíme vypočítat.
