Pythagorova věta + objem - příklady a úlohy
Počet nalezených příkladů: 290
- Těžítko 3
 Těžítko ze skla má tvar pravidelného čtyřbokého jehlanu o hraně podstavy 10cm. Stěny pláště jsou rovnostranné trojúhelníky. Jakou hmotnost v gramech má těžítko, jestliže hustota skla je 2500kg/m³?
Těžítko ze skla má tvar pravidelného čtyřbokého jehlanu o hraně podstavy 10cm. Stěny pláště jsou rovnostranné trojúhelníky. Jakou hmotnost v gramech má těžítko, jestliže hustota skla je 2500kg/m³? - Obvod 34
 Obvod podstavy pravidelného čtyřbokého jehlanu je stejně velký jako jeho výška. Jehlan má objem 288 dm³. Vypočítejte jeho povrch. Výsledek zaokrouhlete na celé dm².
Obvod podstavy pravidelného čtyřbokého jehlanu je stejně velký jako jeho výška. Jehlan má objem 288 dm³. Vypočítejte jeho povrch. Výsledek zaokrouhlete na celé dm². - Vypočítejte 248
 Vypočítejte objem a povrch pravidelného čtyřbokého hranolu o podstavné hraně a=24 cm, jestliže tělesová úhlopříčka svírá s podstavou úhel 66°
Vypočítejte objem a povrch pravidelného čtyřbokého hranolu o podstavné hraně a=24 cm, jestliže tělesová úhlopříčka svírá s podstavou úhel 66° - Povrch 32
 Povrch rotačního kužele a obsah jeho podstavy jsou v poměru 18:5. Určete objem kužele, je-li jeho tělesná výška 12 cm.
Povrch rotačního kužele a obsah jeho podstavy jsou v poměru 18:5. Určete objem kužele, je-li jeho tělesná výška 12 cm.
- Načrtni 2
 Načrtni kulovou vrstvu vzniklou z koule o poloměru: r= 8,5cm, je-li dáno: v=1,5cm, r1=7,7cm, r2=6,8cm. Jaký je její objem?
Načrtni kulovou vrstvu vzniklou z koule o poloměru: r= 8,5cm, je-li dáno: v=1,5cm, r1=7,7cm, r2=6,8cm. Jaký je její objem? - Do rovnostranného 2
 Do rovnostranného kužele s průměrem podstavy 12 cm je vepsána koule. Vypočtěte objem obou těles. Kolik procent objemu kužele vyplňuje vepsaná koule?
Do rovnostranného kužele s průměrem podstavy 12 cm je vepsána koule. Vypočtěte objem obou těles. Kolik procent objemu kužele vyplňuje vepsaná koule? - Kulová úseč 4
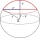 Vypočítejte objem kulové úseče a povrch vrchlíku. Je-li poloměr koule r=5cm a poloměr kruhové podstavy úseče ρ=4cm.
Vypočítejte objem kulové úseče a povrch vrchlíku. Je-li poloměr koule r=5cm a poloměr kruhové podstavy úseče ρ=4cm. - Je dán 25
 Je dán rotační kužel s výškou 18 cm a délkou boční strany s = 45 cm. Vypočtěte povrch a objem
Je dán rotační kužel s výškou 18 cm a délkou boční strany s = 45 cm. Vypočtěte povrch a objem - Vypočítej 391
 Vypočítej objem pravidelného čtyřbokého jehlanu s podstavou čtverce o straně a = 3 cm a délkou boční hrany b = 7 cm
Vypočítej objem pravidelného čtyřbokého jehlanu s podstavou čtverce o straně a = 3 cm a délkou boční hrany b = 7 cm
- Je dán 26
 Je dán rotační kužel s poloměrem 32 cm a délkou boční strany s = 65 cm. Vypočtěte povrch a objem
Je dán rotační kužel s poloměrem 32 cm a délkou boční strany s = 65 cm. Vypočtěte povrch a objem - Vypočtěte 26
 Vypočtěte objem a povrch hranolu s podstavou pravoúhlého trojúhelníka s odvěsnami o délce 40 a 43 cm. Výška hranolu je 60 cm.
Vypočtěte objem a povrch hranolu s podstavou pravoúhlého trojúhelníka s odvěsnami o délce 40 a 43 cm. Výška hranolu je 60 cm. - Z povrchu objem
 Povrch kužele je 75,36 cm, poloměr je 3cm. Vypočítej objem kužele.
Povrch kužele je 75,36 cm, poloměr je 3cm. Vypočítej objem kužele. - Úhlopříčkou 3
 Úhlopříčkou řezu DBFH pravidelného čtyřbokého hranolu ABCDEFGH je vepsán kruh o průměru 8 cm. Jaký je objem hranolu.
Úhlopříčkou řezu DBFH pravidelného čtyřbokého hranolu ABCDEFGH je vepsán kruh o průměru 8 cm. Jaký je objem hranolu. - Vypočítejte 252
 Vypočítejte objem krychle se stěnovou úhlopříčkou u = 20 cm.
Vypočítejte objem krychle se stěnovou úhlopříčkou u = 20 cm.
- Vypočítej 393
 Vypočítej objem a povrch kužele s průměrem podstavy d = 22 cm a tělesovou výškou v = 40 cm
Vypočítej objem a povrch kužele s průměrem podstavy d = 22 cm a tělesovou výškou v = 40 cm - Šestiboký 6
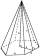 Šestiboký jehlan má obvod 120 cm, délku boční hrany 25 cm. Vypočítej jeho objem.
Šestiboký jehlan má obvod 120 cm, délku boční hrany 25 cm. Vypočítej jeho objem. - Do koule
 Do koule o poloměru 27 cm je vepsána krychle. Vypočtěte její objem a povrch.
Do koule o poloměru 27 cm je vepsána krychle. Vypočtěte její objem a povrch. - Vypočítej 2577
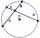 Vypočítej délku tětivy kružnice, která je vzdálena od středu kružnice 2,5 cm. Poloměr je 6,5 cm.
Vypočítej délku tětivy kružnice, která je vzdálena od středu kružnice 2,5 cm. Poloměr je 6,5 cm. - Tětiva 21
 Poloměr kružnice je 5,5 cm. Výška je 2,3 cm a je to vzdálenost tětivy. Délku tětivy máme vypocitat
Poloměr kružnice je 5,5 cm. Výška je 2,3 cm a je to vzdálenost tětivy. Délku tětivy máme vypocitat
Máš úkol, nad kterým si lámeš alespoň 10 minut hlavu? Pošli nám úkol a my Ti ji zkusíme vypočítat.
