Pythagorova věta + Euklidovy věty - příklady a úlohy
Počet nalezených příkladů: 33
- V pravoúhlém 10
 V pravoúhlém trojúhelníku ABC jsou délky odvěsen a = 7,2 cm, b = 10,4 cm. Vypočtěte a) délky úseků přepony b) výšku k přeponě c
V pravoúhlém trojúhelníku ABC jsou délky odvěsen a = 7,2 cm, b = 10,4 cm. Vypočtěte a) délky úseků přepony b) výšku k přeponě c - Euklid 9
 Pomocí Euklidových vět a věty Pythagorovy doplňte následující parametry popisující pravoůhlý trojůhelník ABC s pravým úhlem při vrcholu C, pokud víme b=10, cb=8
Pomocí Euklidových vět a věty Pythagorovy doplňte následující parametry popisující pravoůhlý trojůhelník ABC s pravým úhlem při vrcholu C, pokud víme b=10, cb=8 - V pravoúhlém 8
 V pravoúhlém trojúhelníku ABC (AB je přepona) platí a : b = 24 : 7 a výška na stranu c = 12,6 cm. Vypočítejte délky stran trojúhelníku ABC.
V pravoúhlém trojúhelníku ABC (AB je přepona) platí a : b = 24 : 7 a výška na stranu c = 12,6 cm. Vypočítejte délky stran trojúhelníku ABC. - PT trojuhélnik
 Vypočtěte zbývající strany pravoúhlého trojúhelníku pokud známe b = 4 cm a vc = 2,4cm.
Vypočtěte zbývající strany pravoúhlého trojúhelníku pokud známe b = 4 cm a vc = 2,4cm.
- Euklid 5
 Vypočítejte strany pravoúhlého trojúhelníku ABC pokud: a = 7 cm, vc = 5 cm.
Vypočítejte strany pravoúhlého trojúhelníku ABC pokud: a = 7 cm, vc = 5 cm. - Rovnoramenný IV
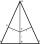 V rovnoramenném trojúhelníku ABC je |AC| = |BC| = 13. |AB| = 10. Vypočtěte poloměr vepsané (r) a opsané (R) kružnice.
V rovnoramenném trojúhelníku ABC je |AC| = |BC| = 13. |AB| = 10. Vypočtěte poloměr vepsané (r) a opsané (R) kružnice. - Důkaz PV
 Lze jednoduše dokázat Pythagorovu větu pomocí Euklidových vět? Pokud ano, dokažte.
Lze jednoduše dokázat Pythagorovu větu pomocí Euklidových vět? Pokud ano, dokažte. - Euklid4
 Odvěsny pravoúhlého trojúhelníku mají rozměry 154 m a 211 m. Vypočítejte délky přepony a výšky na přeponu.
Odvěsny pravoúhlého trojúhelníku mají rozměry 154 m a 211 m. Vypočítejte délky přepony a výšky na přeponu. - Euklidovská vzdálenost
 Vypočítejte euklidovské vzdálenosti mezi prodejnami A, B a C, pokud: A 45 0,05 B 60 0,05 C 52 0,09 Přičemž první údaj je hmotnost pečiva v gramech a druhý je cena pečiva v €.
Vypočítejte euklidovské vzdálenosti mezi prodejnami A, B a C, pokud: A 45 0,05 B 60 0,05 C 52 0,09 Přičemž první údaj je hmotnost pečiva v gramech a druhý je cena pečiva v €.
- Euklid bez euklida
 Mějme pravoúhlý trojúhelník ABC s pravým úhlem při vrcholu C, a = 10, c = 18. Vypočítejte výšku v trojúhelníku na stranu AB bez použití Euklidových vět.
Mějme pravoúhlý trojúhelník ABC s pravým úhlem při vrcholu C, a = 10, c = 18. Vypočítejte výšku v trojúhelníku na stranu AB bez použití Euklidových vět. - Kosočtverec a vepsaná
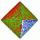 Kosočtverec má stranu a=6 cm, poloměr vepsané kružnice je r=2 cm. Vypočtěte délky obou úhlopříček.
Kosočtverec má stranu a=6 cm, poloměr vepsané kružnice je r=2 cm. Vypočtěte délky obou úhlopříček. - Trojúhelník 32733
 Vypočítej pravoúhlý trojúhelník ABC, odvěsna b=43,5 cm přepona c=72,9 cm. Vypočítej cb, a, ca, v?
Vypočítej pravoúhlý trojúhelník ABC, odvěsna b=43,5 cm přepona c=72,9 cm. Vypočítej cb, a, ca, v? - Vypočítejte 20
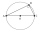 Vypočítejte strany pravoúhlého trojúhelníku, je-li zadána, že a+b=17cm, poloměr vepsané kružnice ρ=2cm.
Vypočítejte strany pravoúhlého trojúhelníku, je-li zadána, že a+b=17cm, poloměr vepsané kružnice ρ=2cm. - Trojúhelník
 V trojúhelníku ABC se stranou BC délky 2 cm je bod K středem strany AB. Body L a M rozdělují stranu AC na tři shodné úsečky. Trojúhelník KLM je rovnoramenný s pravým úhlem u vrcholu K. Určete délky stran AB, AC trojúhelníku ABC.
V trojúhelníku ABC se stranou BC délky 2 cm je bod K středem strany AB. Body L a M rozdělují stranu AC na tři shodné úsečky. Trojúhelník KLM je rovnoramenný s pravým úhlem u vrcholu K. Určete délky stran AB, AC trojúhelníku ABC.
- Trojúhelníku 7216
 Pravý rovnoramenný trojúhelník má výšku x nakreslenou z pravého úhlu k přeponě, která jej rozděluje na dva nestejné segmenty. Délka jednoho segmentu je 5 cm. Jaká je plocha trojúhelníku? Děkuji.
Pravý rovnoramenný trojúhelník má výšku x nakreslenou z pravého úhlu k přeponě, která jej rozděluje na dva nestejné segmenty. Délka jednoho segmentu je 5 cm. Jaká je plocha trojúhelníku? Děkuji. - Poměr odvěsen
 Pro délky odvěsen pravoúhlého trojúhelníku ABC platí a: b = 2:3. Přepona má délku 10 cm. Vypočtěte délky odvěsen toho trojúhelníku.
Pro délky odvěsen pravoúhlého trojúhelníku ABC platí a: b = 2:3. Přepona má délku 10 cm. Vypočtěte délky odvěsen toho trojúhelníku. - V pravoúhlém 2
 V pravoúhlém trojúhelníku ABC jsou známy tyto prvky: a = 10 cm, vc = 9,23 cm. Vypočítejte o, R (poloměr opsané kružnice), r (poloměr vepsané kružnice).
V pravoúhlém trojúhelníku ABC jsou známy tyto prvky: a = 10 cm, vc = 9,23 cm. Vypočítejte o, R (poloměr opsané kružnice), r (poloměr vepsané kružnice). - Kružnice
 V kružnici s poloměrem 7,5 cm jsou sestrojeny 2 rovnoběžné tětivy, jejichž délky jsou 9 cm a 12 cm. Vypočítejte vzdálenost těchto tětiv (pokud jsou možné dvě řešení napište obě).
V kružnici s poloměrem 7,5 cm jsou sestrojeny 2 rovnoběžné tětivy, jejichž délky jsou 9 cm a 12 cm. Vypočítejte vzdálenost těchto tětiv (pokud jsou možné dvě řešení napište obě). - Pravoúhlý Δ
 Pravoúhlý trojúhelník má délku odvěsny 56 cm a délku přepony 70 cm. Vypočítejte výšku trojúhelníku.
Pravoúhlý trojúhelník má délku odvěsny 56 cm a délku přepony 70 cm. Vypočítejte výšku trojúhelníku.
Máš úkol, nad kterým si lámeš alespoň 10 minut hlavu? Pošli nám úkol a my Ti ji zkusíme vypočítat.
