Sčítání + matematická olympiáda - příklady a úlohy
Počet nalezených příkladů: 20
- Myslím 20
 Myslím si tři čísla, když je sečtou dostanu 16, když od součtu prvních dvou čísel odečtou třetí dostanu 10, když od součtu prvního a třetího čísla odečtou druhé dostanu 8. Která čísla si myslím?
Myslím si tři čísla, když je sečtou dostanu 16, když od součtu prvních dvou čísel odečtou třetí dostanu 10, když od součtu prvního a třetího čísla odečtou druhé dostanu 8. Která čísla si myslím? - Představují 82998
 Adam napsal následující součet s pěti tajnými sčítanci: a + bb + ccc + dddd + eeeee. Prozradil, že znaky „a, b, c, d, e“ představují navzájem různé číslice 1, 2, 3, 4, 5 a že výsledný součet je dělitelný 11. Které nejmenší a které největší číslo může být
Adam napsal následující součet s pěti tajnými sčítanci: a + bb + ccc + dddd + eeeee. Prozradil, že znaky „a, b, c, d, e“ představují navzájem různé číslice 1, 2, 3, 4, 5 a že výsledný součet je dělitelný 11. Které nejmenší a které největší číslo může být - Trojciferné 80768
 Nikola měla v sešitě napsáno jedno trojciferné a jedno dvouciferné číslo. Každé z těchto čísel bylo tvořeno navzájem různými číslicemi. Rozdíl Nikoliných čísel byl 976. Jaký byl jejich součet?
Nikola měla v sešitě napsáno jedno trojciferné a jedno dvouciferné číslo. Každé z těchto čísel bylo tvořeno navzájem různými číslicemi. Rozdíl Nikoliných čísel byl 976. Jaký byl jejich součet? - Vierka 3 MO Z8
 Vierka ze tří daných číslic sestavovala navzájem různá trojmístné čísla. Když všechna tato čísla sečetla, vyšlo jí 1221. Jaké číslice Vierka použila? Určete pět možností
Vierka ze tří daných číslic sestavovala navzájem různá trojmístné čísla. Když všechna tato čísla sečetla, vyšlo jí 1221. Jaké číslice Vierka použila? Určete pět možností - 9 z 10 čísel
 Určete počet devítimístných čísel, ve kterých se každá z číslic 0 až 9 vyskytuje nejvíce jednou a v nichž se součty číslic na 1. až 3. místě, na 3. až 5. místě, na 5. až 7. místě a na 7. až 9. místě vždy rovnají 10. Najděte i nejmenší a největší z těchto
Určete počet devítimístných čísel, ve kterých se každá z číslic 0 až 9 vyskytuje nejvíce jednou a v nichž se součty číslic na 1. až 3. místě, na 3. až 5. místě, na 5. až 7. místě a na 7. až 9. místě vždy rovnají 10. Najděte i nejmenší a největší z těchto - Veverky 2
 Veverky objevily keř s lískovými oříšky. První veverka utrhla jeden oříšek, druhá veverka dva oříšky, třetí veverka tři oříšky. Každá další veverka utrhla vždy o jeden oříšek víc než předchozí veverka. Když otrhaly všechny oříšky z keře, rozdělily si oříš
Veverky objevily keř s lískovými oříšky. První veverka utrhla jeden oříšek, druhá veverka dva oříšky, třetí veverka tři oříšky. Každá další veverka utrhla vždy o jeden oříšek víc než předchozí veverka. Když otrhaly všechny oříšky z keře, rozdělily si oříš - Pážata MO Z6-I-4
 Jednou si král zavolal všechna svá pážata a postavil je do řady. Prvnímu pážeti dal určitý počet dukátů, druhému dal o dva dukáty méně, třetímu opět o dva dukáty méně a tak dále. Když došel k poslednímu pážeti, dal mu příslušný počet dukátů, otočil se a o
Jednou si král zavolal všechna svá pážata a postavil je do řady. Prvnímu pážeti dal určitý počet dukátů, druhému dal o dva dukáty méně, třetímu opět o dva dukáty méně a tak dále. Když došel k poslednímu pážeti, dal mu příslušný počet dukátů, otočil se a o - Z8–I–5 MO 2019
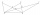 Pro osm navzájem různých bodů jako na obrázku platí, že body C, D, E leží na přímce rovnoběžné s přímkou AB, F je středem úsečky AD, G je středem úsečky AC a H je průsečíkem přímek AC a BE. Obsah trojúhelníku BCG je 12 cm² a obsah čtyřúhelníku DFHG je 8 c
Pro osm navzájem různých bodů jako na obrázku platí, že body C, D, E leží na přímce rovnoběžné s přímkou AB, F je středem úsečky AD, G je středem úsečky AC a H je průsečíkem přímek AC a BE. Obsah trojúhelníku BCG je 12 cm² a obsah čtyřúhelníku DFHG je 8 c - MO Z7–I–3 2019
 Roman má rád kouzla a matematiku. Naposled kouzlil s trojmístnými nebo čtyřmístnými čísly takto: • z daného čísla vytvořil dvě nová čísla tak, že ho rozdělil mezi číslicemi na místě stovek a desítek (např. Z čísla 581 by dostal 5 a 81), • nová čísla sečet
Roman má rád kouzla a matematiku. Naposled kouzlil s trojmístnými nebo čtyřmístnými čísly takto: • z daného čísla vytvořil dvě nová čísla tak, že ho rozdělil mezi číslicemi na místě stovek a desítek (např. Z čísla 581 by dostal 5 a 81), • nová čísla sečet - MO 2019 Z9–I–5
 Majka zkoumala vícemístná čísla, ve kterých se pravidelně střídají liché a sudé číslice. Ta, která začínají lichou číslicí, nazvala komická a ta, která začínají sudou číslicí, nazvala veselá. (Např. Číslo 32387 je komické, číslo 4529 je veselé. ) Majka vy
Majka zkoumala vícemístná čísla, ve kterých se pravidelně střídají liché a sudé číslice. Ta, která začínají lichou číslicí, nazvala komická a ta, která začínají sudou číslicí, nazvala veselá. (Např. Číslo 32387 je komické, číslo 4529 je veselé. ) Majka vy - Samopočet
 Samopočet funguje přesně jako kalkulačka. Hostinský chtěl na samopočte sečíst několik trojmístných přirozených čísel. Na první pokus dostal výsledek 2224. Pro kontrolu sečetl tato čísla znovu a vyšlo mu 2198. Proto sečetl tato čísla ještě jednou a nyní do
Samopočet funguje přesně jako kalkulačka. Hostinský chtěl na samopočte sečíst několik trojmístných přirozených čísel. Na první pokus dostal výsledek 2224. Pro kontrolu sečetl tato čísla znovu a vyšlo mu 2198. Proto sečetl tato čísla ještě jednou a nyní do - Z6–I–5 MO 2018
 V následujícím příkladě na sčítání představují stejná písmena stejné číslice, různá písmena různé číslice. RATAM RAD -------------- ULOHY
V následujícím příkladě na sčítání představují stejná písmena stejné číslice, různá písmena různé číslice. RATAM RAD -------------- ULOHY - Z5 – I – 5
 Tomáš dostal devět kartiček, na nichž byly následující čísla a matematické symboly: 18, 19, 20, 20, +, −, ×, (, ) Kartičky skládal tak, že vedle sebe nikdy neležely dvě kartičky s čísly, tj. Střídaly se kartičky s čísly a kartičky se symboly. Takto vznikl
Tomáš dostal devět kartiček, na nichž byly následující čísla a matematické symboly: 18, 19, 20, 20, +, −, ×, (, ) Kartičky skládal tak, že vedle sebe nikdy neležely dvě kartičky s čísly, tj. Střídaly se kartičky s čísly a kartičky se symboly. Takto vznikl - Z5–I–6 MO 2017
 Na stole leželo osm kartiček s čísly 2, 3, 5, 7, 11, 13, 17, 19. Ferda si vybral tři kartičky. Sečetl na nich napsaná čísla a zjistil, že jejich součet je o 1 větší než součet čísel na zbylých kartičkách. Které kartičky mohly zůstat na stole? Určete všech
Na stole leželo osm kartiček s čísly 2, 3, 5, 7, 11, 13, 17, 19. Ferda si vybral tři kartičky. Sečetl na nich napsaná čísla a zjistil, že jejich součet je o 1 větší než součet čísel na zbylých kartičkách. Které kartičky mohly zůstat na stole? Určete všech - Z9–I–4 MO 2017
 Čísla 1, 2, 3, 4, 5, 6, 7, 8 a 9 se chystala na cestu vlakem se třemi vagóny. Chtěla se rozsadit tak, aby v každém vagóně seděla tři čísla a největší z každé trojice bylo rovno součtu zbylých dvou. Průvodčí tvrdil, že to není problém, a snažil se číslům p
Čísla 1, 2, 3, 4, 5, 6, 7, 8 a 9 se chystala na cestu vlakem se třemi vagóny. Chtěla se rozsadit tak, aby v každém vagóně seděla tři čísla a největší z každé trojice bylo rovno součtu zbylých dvou. Průvodčí tvrdil, že to není problém, a snažil se číslům p - MO Z6-I-2 2017
 Erika chtěla nabídnout čokoládu svým třem kamarádkám. Když ji vytáhla z batohu, zjistila, že je polámaná jako na obrázku. (Vyznačené čtverečky jsou navzájem shodné.) Dívky se dohodly, že čokoládu dále lámat nebudou a losem určí, jak velký kousek která dos
Erika chtěla nabídnout čokoládu svým třem kamarádkám. Když ji vytáhla z batohu, zjistila, že je polámaná jako na obrázku. (Vyznačené čtverečky jsou navzájem shodné.) Dívky se dohodly, že čokoládu dále lámat nebudou a losem určí, jak velký kousek která dos - Z8–I–1 2017 Číslo milion
 Vyjádřete číslo milion (1000000) pomocí čísel obsahujících pouze číslice 9 a algebraických operací plus, minus, krát, děleno, mocnina a odmocnina. Určete alespoň tři různá řešení.
Vyjádřete číslo milion (1000000) pomocí čísel obsahujících pouze číslice 9 a algebraických operací plus, minus, krát, děleno, mocnina a odmocnina. Určete alespoň tři různá řešení. - Osmistěn
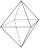 Na každé stěně pravidelného osmistěnu je napsáno jedno z čísel 1, 2, 3, 4, 5, 6, 7 a 8, přičemž na různých stěnách jsou různá čísla. U každé stěny Jarda určil součet čísla na ní napsaného s čísly tří sousedních stěn. Takto dostal osm součtů, které také se
Na každé stěně pravidelného osmistěnu je napsáno jedno z čísel 1, 2, 3, 4, 5, 6, 7 a 8, přičemž na různých stěnách jsou různá čísla. U každé stěny Jarda určil součet čísla na ní napsaného s čísly tří sousedních stěn. Takto dostal osm součtů, které také se - Vláček
 Čísla 1,2,3,4,5,6,7,8 a 9 cestovala vlakem. Vlak měl tři vagony a v každém se vezla právě tři čísla. Číslo 1 se vezlo v prvním vagonu a v posledním vagonu byla všechna čísla lichá. Průvodčí cestou spočítal součet čísel v prvním, druhém i posledním vagonu
Čísla 1,2,3,4,5,6,7,8 a 9 cestovala vlakem. Vlak měl tři vagony a v každém se vezla právě tři čísla. Číslo 1 se vezlo v prvním vagonu a v posledním vagonu byla všechna čísla lichá. Průvodčí cestou spočítal součet čísel v prvním, druhém i posledním vagonu - Betka
 Betka si myslela přirozené číslo s navzájem různými ciframi a napsala ho na tabuli. Pod něj zapsala cifry původního čísla odzadu a tak získala nové číslo. Sečtením těchto dvou čísel dostala číslo, které mělo stejný počet cifer jako myšleny číslo a skládal
Betka si myslela přirozené číslo s navzájem různými ciframi a napsala ho na tabuli. Pod něj zapsala cifry původního čísla odzadu a tak získala nové číslo. Sečtením těchto dvou čísel dostala číslo, které mělo stejný počet cifer jako myšleny číslo a skládal
Máš úkol, nad kterým si lámeš alespoň 10 minut hlavu? Pošli nám úkol a my Ti ji zkusíme vypočítat.
