Trojúhelník + objem - příklady a úlohy
Počet nalezených příkladů: 345
- Trojboký hranol
 Vypočítejte objem pravidelného trojbokého hranolu, jehož výška je rovna délce podstavné hrany. Objem vypočítejte pro délku hrany a = 6 cm.
Vypočítejte objem pravidelného trojbokého hranolu, jehož výška je rovna délce podstavné hrany. Objem vypočítejte pro délku hrany a = 6 cm. - Do rovnostranného 2
 Do rovnostranného kužele s průměrem podstavy 12 cm je vepsána koule. Vypočtěte objem obou těles. Kolik procent objemu kužele vyplňuje vepsaná koule?
Do rovnostranného kužele s průměrem podstavy 12 cm je vepsána koule. Vypočtěte objem obou těles. Kolik procent objemu kužele vyplňuje vepsaná koule? - Je dán 25
 Je dán rotační kužel s výškou 18 cm a délkou boční strany s = 45 cm. Vypočtěte povrch a objem
Je dán rotační kužel s výškou 18 cm a délkou boční strany s = 45 cm. Vypočtěte povrch a objem - Je dán 26
 Je dán rotační kužel s poloměrem 32 cm a délkou boční strany s = 65 cm. Vypočtěte povrch a objem
Je dán rotační kužel s poloměrem 32 cm a délkou boční strany s = 65 cm. Vypočtěte povrch a objem - Vypočtěte 26
 Vypočtěte objem a povrch hranolu s podstavou pravoúhlého trojúhelníka s odvěsnami o délce 40 a 43 cm. Výška hranolu je 60 cm.
Vypočtěte objem a povrch hranolu s podstavou pravoúhlého trojúhelníka s odvěsnami o délce 40 a 43 cm. Výška hranolu je 60 cm. - Rs3 hranol
 Vypočtěte objem a povrch hranolu o výšce 9,6 cm s podstavou rovnostranného trojúhelníka o straně délky 4,8 cm.
Vypočtěte objem a povrch hranolu o výšce 9,6 cm s podstavou rovnostranného trojúhelníka o straně délky 4,8 cm. - Skleník 2
 Skleník má tvar hranolu položeného na boční stěně. Podstavu tvoří lichoběžník a trojúhelník. Dolní základna lichoběžníku má délku 3 m, horní základna (a strana trojúhelníku) má délku 2 m, výška lichoběžníku je 1,8 m a výška trojúhelníku je 0,6 m. Výška hr
Skleník má tvar hranolu položeného na boční stěně. Podstavu tvoří lichoběžník a trojúhelník. Dolní základna lichoběžníku má délku 3 m, horní základna (a strana trojúhelníku) má délku 2 m, výška lichoběžníku je 1,8 m a výška trojúhelníku je 0,6 m. Výška hr - Spádnice
 Určit objem a povrch kužele, jehož spádnice o délce 8cm svírá s rovinou podstavy úhel 75 stupňů
Určit objem a povrch kužele, jehož spádnice o délce 8cm svírá s rovinou podstavy úhel 75 stupňů - Těžítko 3
 Těžítko ze skla má tvar pravidelného čtyřbokého jehlanu o hraně podstavy 10cm. Stěny pláště jsou rovnostranné trojúhelníky. Jakou hmotnost v gramech má těžítko, jestliže hustota skla je 2500kg/m³?
Těžítko ze skla má tvar pravidelného čtyřbokého jehlanu o hraně podstavy 10cm. Stěny pláště jsou rovnostranné trojúhelníky. Jakou hmotnost v gramech má těžítko, jestliže hustota skla je 2500kg/m³? - Vypočítej 391
 Vypočítej objem pravidelného čtyřbokého jehlanu s podstavou čtverce o straně a = 3 cm a délkou boční hrany b = 7 cm
Vypočítej objem pravidelného čtyřbokého jehlanu s podstavou čtverce o straně a = 3 cm a délkou boční hrany b = 7 cm - Vypočítejte 248
 Vypočítejte objem a povrch pravidelného čtyřbokého hranolu o podstavné hraně a=24 cm, jestliže tělesová úhlopříčka svírá s podstavou úhel 66°
Vypočítejte objem a povrch pravidelného čtyřbokého hranolu o podstavné hraně a=24 cm, jestliže tělesová úhlopříčka svírá s podstavou úhel 66° - Šestiboký 6
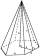 Šestiboký jehlan má obvod 120 cm, délku boční hrany 25 cm. Vypočítej jeho objem.
Šestiboký jehlan má obvod 120 cm, délku boční hrany 25 cm. Vypočítej jeho objem. - Kulová úseč 4
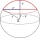 Vypočítejte objem kulové úseče a povrch vrchlíku. Je-li poloměr koule r=5cm a poloměr kruhové podstavy úseče ρ=4cm.
Vypočítejte objem kulové úseče a povrch vrchlíku. Je-li poloměr koule r=5cm a poloměr kruhové podstavy úseče ρ=4cm. - Úhlopříčkou 3
 Úhlopříčkou řezu DBFH pravidelného čtyřbokého hranolu ABCDEFGH je vepsán kruh o průměru 8 cm. Jaký je objem hranolu.
Úhlopříčkou řezu DBFH pravidelného čtyřbokého hranolu ABCDEFGH je vepsán kruh o průměru 8 cm. Jaký je objem hranolu. - Vypočítejte 228
 Vypočítejte, kolik hl vody se vejde do padesátimetrového zkoseného bazénu, jestliže nejmenší hloubka je 1,2 m a největší hloubka je 3 m, šířka bazénu je 20 m. Dle vypočítejte, kolik kachlíčků tvaru čtverce o délce strany 15 cm je třeba k vykachlíčkování s
Vypočítejte, kolik hl vody se vejde do padesátimetrového zkoseného bazénu, jestliže nejmenší hloubka je 1,2 m a největší hloubka je 3 m, šířka bazénu je 20 m. Dle vypočítejte, kolik kachlíčků tvaru čtverce o délce strany 15 cm je třeba k vykachlíčkování s - Trojúhelníku 65674
 Obvod trojúhelníku je 125 cm. Nejkratší strana je o 12 cm kratší než nejdelší strana. Nejdelší strana je o 7 cm delší než střední strana. Jak dlouhá je střední strana?
Obvod trojúhelníku je 125 cm. Nejkratší strana je o 12 cm kratší než nejdelší strana. Nejdelší strana je o 7 cm delší než střední strana. Jak dlouhá je střední strana? - Trojúhelníku 64814
 Dvě strany trojúhelníku mají délky stran a=6cm, b=13cm. Potom pro délku třetí strany c platí: (A) 7
Dvě strany trojúhelníku mají délky stran a=6cm, b=13cm. Potom pro délku třetí strany c platí: (A) 7 - Trojboký hranol 8
 Jen dán pravidelný trojboký hranol s hranou podstavy 20dm a výškou 30dm. Vypočítejte objem hranolu a obsah pláště.
Jen dán pravidelný trojboký hranol s hranou podstavy 20dm a výškou 30dm. Vypočítejte objem hranolu a obsah pláště. - Nádoba - kužel
 Uzavřená nádoba ve tvaru kužele stojící na své podstavě je naplněna vodou tak, že hladina se nachází 8 cm od vrcholu. Po otočení nádoby o 180 stupňů – stojí na vrcholu – je hladina vzdálena 2 cm od podstavy. Jak vysoká nádoba je?
Uzavřená nádoba ve tvaru kužele stojící na své podstavě je naplněna vodou tak, že hladina se nachází 8 cm od vrcholu. Po otočení nádoby o 180 stupňů – stojí na vrcholu – je hladina vzdálena 2 cm od podstavy. Jak vysoká nádoba je? - Trojboký jehlan
 Určete objem a povrch pravidelného trojbokého jehlanu, který má podstavnou hranu a = 20 cm a boční hranu b = 35 cm
Určete objem a povrch pravidelného trojbokého jehlanu, který má podstavnou hranu a = 20 cm a boční hranu b = 35 cm
Máš úkol, nad kterým si lámeš alespoň 10 minut hlavu? Pošli nám úkol a my Ti ji zkusíme vypočítat.
