Příklady na obsah úhel
Počet nalezených příkladů: 219
- Tangens 2
 Tangens úhlu tvořeného sousedními stranami trojúhelníka ABC (strana a=29 m, b = 40 m) je roven 1,05. Spočítejte obsah toho trojúhelníka.
Tangens úhlu tvořeného sousedními stranami trojúhelníka ABC (strana a=29 m, b = 40 m) je roven 1,05. Spočítejte obsah toho trojúhelníka. - Uhly lich
 Je dan lichobeznik ABCD a velikosti vnitřních úhlů. Úhel SDC 32° Úhel SAD 33° Úhel SDA 77° Úhel CBS 29°, kde S je průsečnik uhlopříček. Jaká je velikost úhlu BSA?
Je dan lichobeznik ABCD a velikosti vnitřních úhlů. Úhel SDC 32° Úhel SAD 33° Úhel SDA 77° Úhel CBS 29°, kde S je průsečnik uhlopříček. Jaká je velikost úhlu BSA? - Spádnice
 Určit objem a povrch kužele, jehož spádnice o délce 8cm svírá s rovinou podstavy úhel 75 stupňů
Určit objem a povrch kužele, jehož spádnice o délce 8cm svírá s rovinou podstavy úhel 75 stupňů - Vypočítejte 248
 Vypočítejte objem a povrch pravidelného čtyřbokého hranolu o podstavné hraně a=24 cm, jestliže tělesová úhlopříčka svírá s podstavou úhel 66°
Vypočítejte objem a povrch pravidelného čtyřbokého hranolu o podstavné hraně a=24 cm, jestliže tělesová úhlopříčka svírá s podstavou úhel 66° - Kruhová 4
 Kruhová úseč má obsah 6,04 cm², středový úhel omega je 15 stupňů, jaký je poloměr?
Kruhová úseč má obsah 6,04 cm², středový úhel omega je 15 stupňů, jaký je poloměr? - Podobnost
 Obsah pravidelného 10-úhelníka je 563 cm². Obsah jemu podobného 10-úhelníka je 949 dm². Určete poměr podobnosti.
Obsah pravidelného 10-úhelníka je 563 cm². Obsah jemu podobného 10-úhelníka je 949 dm². Určete poměr podobnosti. - Setrvačnosti 81906
 Jakou energii dodal setrvačník zařízení pokud počet jeho otáček klesl z 1200 na 720 otáček za minutu, má-li moment setrvačnosti 71,3 kg/m²?
Jakou energii dodal setrvačník zařízení pokud počet jeho otáček klesl z 1200 na 720 otáček za minutu, má-li moment setrvačnosti 71,3 kg/m²? - Obsah a úhly
 Vypočítej velikosti všech stran a vnitřních úhlů trojúhelníku ABC, jestliže je dáno: S = 501,9; α = 15°28' a β = 45°.
Vypočítej velikosti všech stran a vnitřních úhlů trojúhelníku ABC, jestliže je dáno: S = 501,9; α = 15°28' a β = 45°. - Parametrické 2595
 Vypočítat vnitřní úhly trojúhelníku ABC pomocí vektorů. Souřadnice A[2;4] B[4;6] C[0;-4]. Vypočítat směrové vektory stran, parametrické a obecně rovnice stran, parametrické a obecné rovnice těžnic, vypočítat obsah, vypočítat výšku.
Vypočítat vnitřní úhly trojúhelníku ABC pomocí vektorů. Souřadnice A[2;4] B[4;6] C[0;-4]. Vypočítat směrové vektory stran, parametrické a obecně rovnice stran, parametrické a obecné rovnice těžnic, vypočítat obsah, vypočítat výšku. - Vypočítej z ťežnice
 Vypočítej obvod, obsah a velikosti zbývajících úhlů trojúhelníku ABC, jestliže je dáno: a = 8,4; β = 105°35'; ťežnice ta = 12,5.
Vypočítej obvod, obsah a velikosti zbývajících úhlů trojúhelníku ABC, jestliže je dáno: a = 8,4; β = 105°35'; ťežnice ta = 12,5. - Rovnostranný 3-uhelník
 Vypočítejte stranu rovnostranného trojúhelníku, jestliže jeho obsah je 1353 cm².
Vypočítejte stranu rovnostranného trojúhelníku, jestliže jeho obsah je 1353 cm². - Trojúhelník Suu
 Trojúhelník má jednu stranu dlouhou 71 m a jeho dva vnitřní úhly mají velikost 60°. Vypočítejte obvod a obsah trojúhelníku.
Trojúhelník má jednu stranu dlouhou 71 m a jeho dva vnitřní úhly mají velikost 60°. Vypočítejte obvod a obsah trojúhelníku. - Rovnostranný trojúhelník v2
 Rovnostranný trojúhelník má obvod 36 dm. Jaký má obsah?
Rovnostranný trojúhelník má obvod 36 dm. Jaký má obsah? - Úhlopříčka
 Úhlopříčka obdélníku má délku 36,1 cm a svírá s delší stranou úhel 31°. Vypočítejte obsah obdélníku.
Úhlopříčka obdélníku má délku 36,1 cm a svírá s delší stranou úhel 31°. Vypočítejte obsah obdélníku. - Lichoběžník - úhlopříčky
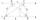 Lichoběžník má délku úhlopříčky AC přeseknutu úhlopříčkou BD v poměru 2:1. Trojúhelník vytvořen body A, průnikem úhlopříček (S) a bodem D má obsah 164 cm². (Tomuto trojúhelníku také patří strana úhlopříčky AC a je 2x větší než její druhá část.) Jaký je ob
Lichoběžník má délku úhlopříčky AC přeseknutu úhlopříčkou BD v poměru 2:1. Trojúhelník vytvořen body A, průnikem úhlopříček (S) a bodem D má obsah 164 cm². (Tomuto trojúhelníku také patří strana úhlopříčky AC a je 2x větší než její druhá část.) Jaký je ob - Pravidelného 4905
 Květinový záhon má tvar pravidelného 4-bokého jehlanu. Hrana dolní podstavy je 10m, horní podstavy je 9m. Odchylka boční stěny od podstavy je 45 stupňů. Kolik sázení je třeba nakoupit, pokud k vysazení 1m čtverečního je třeba 90?
Květinový záhon má tvar pravidelného 4-bokého jehlanu. Hrana dolní podstavy je 10m, horní podstavy je 9m. Odchylka boční stěny od podstavy je 45 stupňů. Kolik sázení je třeba nakoupit, pokud k vysazení 1m čtverečního je třeba 90? - Trojúhelník ABC a TRN
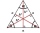 V rovnostranném trojúhelníku ABC je bod T jeho těžištěm, bod R je obrazem bodu T v osové souměrnosti podle přímky AB a bod N je obrazem bodu T v osové souměrnosti podle přímky BC. Určitě poměr obsahů trojúhelníků ABC a TRN.
V rovnostranném trojúhelníku ABC je bod T jeho těžištěm, bod R je obrazem bodu T v osové souměrnosti podle přímky AB a bod N je obrazem bodu T v osové souměrnosti podle přímky BC. Určitě poměr obsahů trojúhelníků ABC a TRN. - Ťežišťe a obsah
 V trojúhelníku ABC jsou dány délky jeho těžnic tc = 9, ta = 6. Označme T průsečík těžnic, S střed strany BC. Velikost úhlu CTS je 60°. Vypočítejte délku strany BC s přesností na 2 desetinná místa.
V trojúhelníku ABC jsou dány délky jeho těžnic tc = 9, ta = 6. Označme T průsečík těžnic, S střed strany BC. Velikost úhlu CTS je 60°. Vypočítejte délku strany BC s přesností na 2 desetinná místa. - SSH trojuholnik
 Vypočítejte obsah trojúhelníku ABC, pokud je dané alfa = 49°, beta = 31° a výška na stranu c je 9cm.
Vypočítejte obsah trojúhelníku ABC, pokud je dané alfa = 49°, beta = 31° a výška na stranu c je 9cm. - Délky stran a úhly
 Vypočtěte délky stran a úhly v pravoúhlém trojúhelníku. S = 210, o = 70.
Vypočtěte délky stran a úhly v pravoúhlém trojúhelníku. S = 210, o = 70.
Máš úkol, nad kterým si lámeš alespoň 10 minut hlavu? Pošli nám úkol a my Ti ji zkusíme vypočítat.
