Matematická olympiáda - 6. ročník - příklady a úlohy
Počet nalezených příkladů: 51
- Z6–I–5 MO 2024
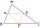 Péťa složil z navzájem shodných trojúhelníků několik rovinných útvarů. Obvody prvních tří jsou postupně 8 cm, 11,4 cm a 14,7 cm. Určete obvod čtvrtého útvaru
Péťa složil z navzájem shodných trojúhelníků několik rovinných útvarů. Obvody prvních tří jsou postupně 8 cm, 11,4 cm a 14,7 cm. Určete obvod čtvrtého útvaru - Pravoúhlý 37
 Pravoúhlý trojúhelník má obsah 36 cm². V něm je umístěn čtverec tak, že dvě strany čtverce jsou částmi dvou stran trojúhelníku a jeden vrchol čtverce je ve třetině nejdelší strany. Určete obsah tohoto čtverce.
Pravoúhlý trojúhelník má obsah 36 cm². V něm je umístěn čtverec tak, že dvě strany čtverce jsou částmi dvou stran trojúhelníku a jeden vrchol čtverce je ve třetině nejdelší strany. Určete obsah tohoto čtverce. - Z6-I-3 2022
 Magda si vystřihla dva stejné rovnoramenné trojúhelníky, z nichž každý měl obvod 100 cm. Nejprve z těchto trojúhelníků složila čtyřúhelník tak, že je k sobě přiložila rameny. Poté z nich složila čtyřúhelník tak, že je k sobě přiložila základnami. V prvním
Magda si vystřihla dva stejné rovnoramenné trojúhelníky, z nichž každý měl obvod 100 cm. Nejprve z těchto trojúhelníků složila čtyřúhelník tak, že je k sobě přiložila rameny. Poté z nich složila čtyřúhelník tak, že je k sobě přiložila základnami. V prvním - Představují 82998
 Adam napsal následující součet s pěti tajnými sčítanci: a + bb + ccc + dddd + eeeee. Prozradil, že znaky „a, b, c, d, e“ představují navzájem různé číslice 1, 2, 3, 4, 5 a že výsledný součet je dělitelný 11. Které nejmenší a které největší číslo může být
Adam napsal následující součet s pěti tajnými sčítanci: a + bb + ccc + dddd + eeeee. Prozradil, že znaky „a, b, c, d, e“ představují navzájem různé číslice 1, 2, 3, 4, 5 a že výsledný součet je dělitelný 11. Které nejmenší a které největší číslo může být - Polovina 80757
 Na louce bylo 45 ovcí a několik pastýřů. Poté, co z louky odešla polovina pastevců a třetina ovcí, měli zbylí pastevci a ovce celkem 126 nohou. Všechny ovce a všichni pastevci měli obvykle počty nohou. kolik pastýřů bylo původně na louce?
Na louce bylo 45 ovcí a několik pastýřů. Poté, co z louky odešla polovina pastevců a třetina ovcí, měli zbylí pastevci a ovce celkem 126 nohou. Všechny ovce a všichni pastevci měli obvykle počty nohou. kolik pastýřů bylo původně na louce? - Z6–I–4 MO 2021/22
 Kuba si zapsal čtyřmístné číslo, jehož 2 číslice byly sudé a dvě liché. Pokud by v tomto čísle vyškrtl obě sudé číslice, dostal by číslo čtyřikrát menší, než kdyby v tomtéž čísle vyškrtl obě liché číslice. Které největší číslo s těmito vlastnostmi si mohl
Kuba si zapsal čtyřmístné číslo, jehož 2 číslice byly sudé a dvě liché. Pokud by v tomto čísle vyškrtl obě sudé číslice, dostal by číslo čtyřikrát menší, než kdyby v tomtéž čísle vyškrtl obě liché číslice. Které největší číslo s těmito vlastnostmi si mohl - Ovce 3
 Kuba se domluvil s bačou, že se mu bude starat o ovce. Bača Kubovi slíbil, že po roce služby dostane dvacet zlatých a k tomu jednu ovci. Jenže Kuba dal výpověď, právě když uplynul sedmý měsíc služby. I tak ho Bača spravedlivě odměnil a zaplatil mu pět zla
Kuba se domluvil s bačou, že se mu bude starat o ovce. Bača Kubovi slíbil, že po roce služby dostane dvacet zlatých a k tomu jednu ovci. Jenže Kuba dal výpověď, právě když uplynul sedmý měsíc služby. I tak ho Bača spravedlivě odměnil a zaplatil mu pět zla - Z6–I–5 MO 2019
 Útvar na obrázku vznikl tak, že z velkého kříže byl vystřižen malý kříž. Každý z těchto křížů může být složen z pěti shodných čtverců, přičemž strany malých čtverců jsou poloviční vzhledem ke stranám velkých čtverců. Obsah šedého útvaru na obrázku je 45 c
Útvar na obrázku vznikl tak, že z velkého kříže byl vystřižen malý kříž. Každý z těchto křížů může být složen z pěti shodných čtverců, přičemž strany malých čtverců jsou poloviční vzhledem ke stranám velkých čtverců. Obsah šedého útvaru na obrázku je 45 c - Pážata MO Z6-I-4
 Jednou si král zavolal všechna svá pážata a postavil je do řady. Prvnímu pážeti dal určitý počet dukátů, druhému dal o dva dukáty méně, třetímu opět o dva dukáty méně a tak dále. Když došel k poslednímu pážeti, dal mu příslušný počet dukátů, otočil se a o
Jednou si král zavolal všechna svá pážata a postavil je do řady. Prvnímu pážeti dal určitý počet dukátů, druhému dal o dva dukáty méně, třetímu opět o dva dukáty méně a tak dále. Když došel k poslednímu pážeti, dal mu příslušný počet dukátů, otočil se a o - Z6 – I – 6 MO 2019
 Majka zkoumala vícemístná čísla, ve kterých se pravidelně střídají liché a sudé číslice. Ta, která začínají lichou číslicí, nazvala komická a ta, která začínají sudou číslicí, nazvala veselá. (Např. Číslo 32387 je komické, číslo 4529 je veselé. ) Mezi tro
Majka zkoumala vícemístná čísla, ve kterých se pravidelně střídají liché a sudé číslice. Ta, která začínají lichou číslicí, nazvala komická a ta, která začínají sudou číslicí, nazvala veselá. (Např. Číslo 32387 je komické, číslo 4529 je veselé. ) Mezi tro - Dědo MO Z5–I–5 2019
 Dědeček má v zahradě tři jabloně a na nich celkem 39 jablek. Jablka rostou jen na osmi větvích: na jedné jabloni plodí dvě větve, na dvou jabloních plodí po třech větvích. Na různých větvích jsou různé počty jablek, ale na každé jabloni je stejný počet ja
Dědeček má v zahradě tři jabloně a na nich celkem 39 jablek. Jablka rostou jen na osmi větvích: na jedné jabloni plodí dvě větve, na dvou jabloních plodí po třech větvích. Na různých větvích jsou různé počty jablek, ale na každé jabloni je stejný počet ja - MO 2019 Z5–I–3 Dukáty
 Pan král rozdával svým synům dukáty. Nejstaršímu synovi dal určitý počet dukátů, mladšímu dal o jeden dukát méně, dalšímu dal opět o jeden dukát méně a takto postupoval až k nejmladšímu. Poté se vrátil k nejstaršímu synovi, dal mu o jeden dukát méně než p
Pan král rozdával svým synům dukáty. Nejstaršímu synovi dal určitý počet dukátů, mladšímu dal o jeden dukát méně, dalšímu dal opět o jeden dukát méně a takto postupoval až k nejmladšímu. Poté se vrátil k nejstaršímu synovi, dal mu o jeden dukát méně než p - MO Z6–I–3 2018
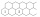 Na obrazku jsou naznačeny dvě řady šestiúhelníkových pole které doprava pokračují bez omezení do každého pole doplňte jedno kladné celé číslo tak aby součet čísel v libovolných třech navzájem sousedících polích byl 2018. Určete číslo které bude 2019 políč
Na obrazku jsou naznačeny dvě řady šestiúhelníkových pole které doprava pokračují bez omezení do každého pole doplňte jedno kladné celé číslo tak aby součet čísel v libovolných třech navzájem sousedících polích byl 2018. Určete číslo které bude 2019 políč - Z6–I–5 MO 2018
 V následujícím příkladě na sčítání představují stejná písmena stejné číslice, různá písmena různé číslice. RATAM RAD -------------- ULOHY
V následujícím příkladě na sčítání představují stejná písmena stejné číslice, různá písmena různé číslice. RATAM RAD -------------- ULOHY - Z6-I-6 MO 2018
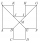 Ve dvanáctiúhelníku ABCDEF GHIJKL jsou každé dvě sousední strany kolmé a všechny strany s výjimkou stran AL a GF jsou navzájem shodné. Strany AL a GF jsou oproti ostatním stranám dvojnásobně dlouhé. Úsečky BG a EL se protínají v bodě M a rozdělují dvanáct
Ve dvanáctiúhelníku ABCDEF GHIJKL jsou každé dvě sousední strany kolmé a všechny strany s výjimkou stran AL a GF jsou navzájem shodné. Strany AL a GF jsou oproti ostatním stranám dvojnásobně dlouhé. Úsečky BG a EL se protínají v bodě M a rozdělují dvanáct - Z6-1-4 MO 2018
 Pan Petřík má na zahradě 3 trpaslíky. Největší je Mašík, prostřední Jířa a nejmenší Faltýnek. Když postaví Faltýnka na Jířu jsou stejně vysocí jako Mašík. Když postaví Faltýnka na Mašíka měří o 34 cm více než Jířa. Když postaví na Mašíka Jířu, jsou o 72 c
Pan Petřík má na zahradě 3 trpaslíky. Největší je Mašík, prostřední Jířa a nejmenší Faltýnek. Když postaví Faltýnka na Jířu jsou stejně vysocí jako Mašík. Když postaví Faltýnka na Mašíka měří o 34 cm více než Jířa. Když postaví na Mašíka Jířu, jsou o 72 c - Z6–I–1 MO 2018
 Ivan a Mirka se dělili o hrušky na míse. Ivan si bere dvě hrušky a Mirka polovinu toho co na míse zbývá. Takto postupně odebírali Ivan, Mirka, Ivan, Mirka a nakonec Ivan, který vzal poslední dvě hrušky. Určete, kdo měl nakonec víc hrušek a o kolik.
Ivan a Mirka se dělili o hrušky na míse. Ivan si bere dvě hrušky a Mirka polovinu toho co na míse zbývá. Takto postupně odebírali Ivan, Mirka, Ivan, Mirka a nakonec Ivan, který vzal poslední dvě hrušky. Určete, kdo měl nakonec víc hrušek a o kolik. - Z5–I–4 MO 2018
 V klubovně byly jen židle a stůl. Každá židle měla čtyři nohy, stůl byl trojnohý. Do klubovny přišli skauti. Každý si sedl na svou židli, dvě židle zůstaly neobsazené a počet nohou v místnosti byl 101. Kolik židlí bylo v klubovně?
V klubovně byly jen židle a stůl. Každá židle měla čtyři nohy, stůl byl trojnohý. Do klubovny přišli skauti. Každý si sedl na svou židli, dvě židle zůstaly neobsazené a počet nohou v místnosti byl 101. Kolik židlí bylo v klubovně? - Z7-1-3 MO 2018
 Děda připravil pro svých šest vnoučat hromádku lískových oříšků s tím, ať si je nějak rozeberou. První přišel Adam, odpočítal si polovinu, přibral si ještě jeden oříšek a odešel. Stejně se zachoval druhý Bob, třetí Cyril, čtvrtý Dan i pátý Eda. Jen Franta
Děda připravil pro svých šest vnoučat hromádku lískových oříšků s tím, ať si je nějak rozeberou. První přišel Adam, odpočítal si polovinu, přibral si ještě jeden oříšek a odešel. Stejně se zachoval druhý Bob, třetí Cyril, čtvrtý Dan i pátý Eda. Jen Franta - Z bodu
 Z bodu A do B je to 16 km z bodu C do B je to 20 km z bodu C do D je to 19 km kolik kilometru to je z bodu D do bodu A
Z bodu A do B je to 16 km z bodu C do B je to 20 km z bodu C do D je to 19 km kolik kilometru to je z bodu D do bodu A
Máš úkol, nad kterým si lámeš alespoň 10 minut hlavu? Pošli nám úkol a my Ti ji zkusíme vypočítat.
