Kvadratická rovnice - 9. ročník - příklady a úlohy
Počet nalezených příkladů: 219
- Součin 25
 Součin dvou celých čisel, z nichž jedno je o 19 větší než druhé, je roveň číslu 416. Najdete oba činitele.
Součin dvou celých čisel, z nichž jedno je o 19 větší než druhé, je roveň číslu 416. Najdete oba činitele. - Cena 1
 Cena 1 kg hrušek je o 7 korun vyšší než cena 1 kg jablek. Prodejce prodal o 2kg jablek více než hrušek. Za hrušky i jablka utržil shodné částky, a to 420 Kč. Kolik kg jablek a kolik kg hrušek prodal?
Cena 1 kg hrušek je o 7 korun vyšší než cena 1 kg jablek. Prodejce prodal o 2kg jablek více než hrušek. Za hrušky i jablka utržil shodné částky, a to 420 Kč. Kolik kg jablek a kolik kg hrušek prodal? - Součin - zvětšíme
 Je dán součin dvou čísel. Zvětšíme-li prvního činitele o 2 a druhého činitele o dva zmenšíme, zvětší se součin o 4. O kolik se součin změní, když prvního činitele o 3 zmenšíme a druhého činitele o 3 zvětšíme?
Je dán součin dvou čísel. Zvětšíme-li prvního činitele o 2 a druhého činitele o dva zmenšíme, zvětší se součin o 4. O kolik se součin změní, když prvního činitele o 3 zmenšíme a druhého činitele o 3 zvětšíme? - Trojúhelníku 83154
 V pravoúhlém trojúhelníku ABC s pravým úhlem u vrcholu C jsou dány velikosti těžnic ta=5, tb=2√10. Vypočítejte velikosti stran trojúhelníku ABC a poloměr kružnice popsané tomuto trojúhelníku.
V pravoúhlém trojúhelníku ABC s pravým úhlem u vrcholu C jsou dány velikosti těžnic ta=5, tb=2√10. Vypočítejte velikosti stran trojúhelníku ABC a poloměr kružnice popsané tomuto trojúhelníku. - Trojúhelník 83143
 Pravý trojúhelník má obvod 300 cm. Jeho přepona je 130 cm. Jaké jsou délky ostatních stran?
Pravý trojúhelník má obvod 300 cm. Jeho přepona je 130 cm. Jaké jsou délky ostatních stran? - Lichoběžníku 82996
 Obsah lichoběžníku je 132cm². Rozdíl délek obou základen je 6cm, výška je o 2cm delší než kratší základna. Určete v centimetrech velikost výšky lichoběžníku.
Obsah lichoběžníku je 132cm². Rozdíl délek obou základen je 6cm, výška je o 2cm delší než kratší základna. Určete v centimetrech velikost výšky lichoběžníku. - Kosočtverce 82850
 Jak zjistím úhlopříčky kosočtverce, pokud jeho obvod je 80dm a jedna úhlopříčka je 2x větší než druhá?
Jak zjistím úhlopříčky kosočtverce, pokud jeho obvod je 80dm a jedna úhlopříčka je 2x větší než druhá? - Zmenšíme-li 82619
 Při úpravě školního pozemku, ve tvaru obdélníku, deviataci vypočítali zvětšíme-li délku i šířku pozemku o 1m zvětšíme jeho výměru o 22m². Zmenšíme-li délku pozemku o 2m a zvětšíme jeho šířku o 1m zmenší se jeho výměra o 5m². Jaká je výměra školního pozemk
Při úpravě školního pozemku, ve tvaru obdélníku, deviataci vypočítali zvětšíme-li délku i šířku pozemku o 1m zvětšíme jeho výměru o 22m². Zmenšíme-li délku pozemku o 2m a zvětšíme jeho šířku o 1m zmenší se jeho výměra o 5m². Jaká je výměra školního pozemk - Trojúhelník 82416
 Jaké strany má pravoúhlý trojúhelník s obvodem 45 centimetrů as obsahem 67,5 cm²?
Jaké strany má pravoúhlý trojúhelník s obvodem 45 centimetrů as obsahem 67,5 cm²? - Vyhodnoťte 82209
 Vyhodnoťte funkci K(x) = 2x²+3x-2 jaká je hodnota K(½)
Vyhodnoťte funkci K(x) = 2x²+3x-2 jaká je hodnota K(½) - Vzdálenosti 81837
 Dva chataři sousedé mají chaty pod lesem u potoka. Rozhodli se postavit můstek přes potok na místě, které je rovněž vzdáleno od obou chat. Vzdálenost mezi chatami je 230 m, jedna chata je od potoka 120 m a druhá od potoka 85 m. Vzdálenosti se myslí kolmé
Dva chataři sousedé mají chaty pod lesem u potoka. Rozhodli se postavit můstek přes potok na místě, které je rovněž vzdáleno od obou chat. Vzdálenost mezi chatami je 230 m, jedna chata je od potoka 120 m a druhá od potoka 85 m. Vzdálenosti se myslí kolmé - Trojúhelníku 81666
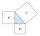 V pravoúhlém trojúhelníku, pokud a =x+34 a b = x a c= 50, pak vyřešte x. Strana c je přepona. Potom diskutujte o případě, kdy a nebo b je přepona.
V pravoúhlém trojúhelníku, pokud a =x+34 a b = x a c= 50, pak vyřešte x. Strana c je přepona. Potom diskutujte o případě, kdy a nebo b je přepona. - Mnohoúhelníku 81587
 Určete druh mnohoúhelníku, je-li počet všech úhlopříček 90. (Zapište počet jeho stran)
Určete druh mnohoúhelníku, je-li počet všech úhlopříček 90. (Zapište počet jeho stran) - Vypočítejte 81138
 Gotický čtyřlístek je ornament, ve kterém jsou do větší kružnice vepsány čtyři stejné dotýkající se menší kružnice, jak vidíte na obrázku. Poloměr velké kružnice je jeden metr. Vypočítejte v metrech poloměr menší kružnice.
Gotický čtyřlístek je ornament, ve kterém jsou do větší kružnice vepsány čtyři stejné dotýkající se menší kružnice, jak vidíte na obrázku. Poloměr velké kružnice je jeden metr. Vypočítejte v metrech poloměr menší kružnice. - Desetinná 80872
 Když se vynásobí dvě desetinná čísla, odpověď je 0,072. Když se sečtou stejná dvě desetinná čísla, odpověď je 0,72. Jaká jsou dvě desetinná čísla?
Když se vynásobí dvě desetinná čísla, odpověď je 0,072. Když se sečtou stejná dvě desetinná čísla, odpověď je 0,72. Jaká jsou dvě desetinná čísla? - Délka 19
 Délka obdélníku je o 1 cm víc než jeho šířka. Jeho obsah je 4 cm². Jaká je jeho šířka?
Délka obdélníku je o 1 cm víc než jeho šířka. Jeho obsah je 4 cm². Jaká je jeho šířka? - Aritmetický 78094
 Najděte hodnotu k tak, aby k² + 2k – 3 byl aritmetický průměr mezi k² + 4k + 5 a k² – 6k + 10.
Najděte hodnotu k tak, aby k² + 2k – 3 byl aritmetický průměr mezi k² + 4k + 5 a k² – 6k + 10. - Motorového 74864
 Rychlostní člun ujede 900 km proti proudu 25 km/h. Cesta mu trvala o 10 minut déle, než by trvala cesta proudem. Jaká je rychlost motorového člunu na stojaté vodě?
Rychlostní člun ujede 900 km proti proudu 25 km/h. Cesta mu trvala o 10 minut déle, než by trvala cesta proudem. Jaká je rychlost motorového člunu na stojaté vodě? - Vypočítejte 74834
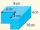 Z jednoho rohu původního kvádru se podle obrázku vyřízne kvádr o hloubce 4 cm, ale délce a šířce x cm (původní kvádr má rozměry 10x8x4 cm). Zbývající tvar má objem 199. Vypočítejte hodnotu x.
Z jednoho rohu původního kvádru se podle obrázku vyřízne kvádr o hloubce 4 cm, ale délce a šířce x cm (původní kvádr má rozměry 10x8x4 cm). Zbývající tvar má objem 199. Vypočítejte hodnotu x. - Vezmeme-li 74704
 Chlapec vypustil z vrchu suché studny minci a za 6 vteřin slyšel zvuk. Vezmeme-li v úvahu, že jde o objekt s volným pádem, jak hluboká je studna? Rychlost zvuku ve vzduchu je přibližně 343 m/s.
Chlapec vypustil z vrchu suché studny minci a za 6 vteřin slyšel zvuk. Vezmeme-li v úvahu, že jde o objekt s volným pádem, jak hluboká je studna? Rychlost zvuku ve vzduchu je přibližně 343 m/s.
Máš úkol, nad kterým si lámeš alespoň 10 minut hlavu? Pošli nám úkol a my Ti ji zkusíme vypočítat.
