Matematická olympiáda - příklady - strana 2 z 11
Úkoly MO nejsou lehké, ani pro dospělé lidi. Zároveň věříme, že správné řešení, které je zde publikované téměř na jeden klik poslouží jen na inspiraci. V reálném životě každý totiž řeší úkoly, které nikdo jiný před tím neřešil.Nenechte se odradit, když neobjevíte hned řešení. Experimentujte, kreslete si, "hrajte se" s úlohou. Někdy pomůže podívat se do nějaké knížky, kde najdete podobné úkoly vyřešeny, jindy se může stát, že najednou o tři dny "z ničeho nic" na řešení přijdete.
Počet nalezených příkladů: 203
- Polovina 80757
 Na louce bylo 45 ovcí a několik pastýřů. Poté, co z louky odešla polovina pastevců a třetina ovcí, měli zbylí pastevci a ovce celkem 126 nohou. Všechny ovce a všichni pastevci měli obvykle počty nohou. kolik pastýřů bylo původně na louce?
Na louce bylo 45 ovcí a několik pastýřů. Poté, co z louky odešla polovina pastevců a třetina ovcí, měli zbylí pastevci a ovce celkem 126 nohou. Všechny ovce a všichni pastevci měli obvykle počty nohou. kolik pastýřů bylo původně na louce? - MO Z9 2022
 Najděte nejmenší kladná čísla a a b, pro které platí 7a³ = 11b⁵
Najděte nejmenší kladná čísla a a b, pro které platí 7a³ = 11b⁵ - Xyz=1400 80562
 Kolik různých množin kladného celého čísla ve tvaru (x, y, z) ke splnění rovnice xyz=1400?
Kolik různých množin kladného celého čísla ve tvaru (x, y, z) ke splnění rovnice xyz=1400? - Z9-I-1 2022
 Bolek a Lolek měli každý svou aritmetickou posloupnost. Jak Lolek, tak Bolek posloupnost začínala číslem 2023 a končila číslem 3023. Tyto dvě posloupnosti měly 26 společných čísel. Poměr Bolkovy a Lolkovy diference byl 5:2. Jaký rozdíl Bolkovy a Lolkovy d
Bolek a Lolek měli každý svou aritmetickou posloupnost. Jak Lolek, tak Bolek posloupnost začínala číslem 2023 a končila číslem 3023. Tyto dvě posloupnosti měly 26 společných čísel. Poměr Bolkovy a Lolkovy diference byl 5:2. Jaký rozdíl Bolkovy a Lolkovy d - Reálného 80499
 V oboru reálných čísel řešte soustavu rovnic: 2x + ⌊y⌋ = 2022, 3y + ⌊2x⌋ = 2023. (⌊a⌋ označuje (dolní) celou část reálného čísla a, tj. největší celé číslo, které není větší než a. Např. ⌊1,9⌋ = 1 a ⌊−1,1⌋ = −2.)
V oboru reálných čísel řešte soustavu rovnic: 2x + ⌊y⌋ = 2022, 3y + ⌊2x⌋ = 2023. (⌊a⌋ označuje (dolní) celou část reálného čísla a, tj. největší celé číslo, které není větší než a. Např. ⌊1,9⌋ = 1 a ⌊−1,1⌋ = −2.) - Matěj 4
 Matěj a Anton jsou staří dohromady 44 let. Matěj je dvakrát tak starý, jako byl Anton v době, když byl Matěj půlkrát tak starý, jako bude Anton, až bude Anton 3x starší, než byl Matěj, když byl Matěj 3x tak starý, jako Anton.
Matěj a Anton jsou staří dohromady 44 let. Matěj je dvakrát tak starý, jako byl Anton v době, když byl Matěj půlkrát tak starý, jako bude Anton, až bude Anton 3x starší, než byl Matěj, když byl Matěj 3x tak starý, jako Anton. - Z6–I–4 MO 2021/22
 Kuba si zapsal čtyřmístné číslo, jehož 2 číslice byly sudé a dvě liché. Pokud by v tomto čísle vyškrtl obě sudé číslice, dostal by číslo čtyřikrát menší, než kdyby v tomtéž čísle vyškrtl obě liché číslice. Které největší číslo s těmito vlastnostmi si mohl
Kuba si zapsal čtyřmístné číslo, jehož 2 číslice byly sudé a dvě liché. Pokud by v tomto čísle vyškrtl obě sudé číslice, dostal by číslo čtyřikrát menší, než kdyby v tomtéž čísle vyškrtl obě liché číslice. Které největší číslo s těmito vlastnostmi si mohl - Postavit 64304
 Kolika různými způsoby se mohou postavit do řady v jídelně Anka, Betka, Cyril, Daniel a Erik, pokud kluci pustí obě dívky před sebe?
Kolika různými způsoby se mohou postavit do řady v jídelně Anka, Betka, Cyril, Daniel a Erik, pokud kluci pustí obě dívky před sebe? - Dvouciferných 64294
 Kolik je přirozených dvouciferných čísel, které můžeme utvořit z číslic 0, 1, 2, 3, pokud se v těchto číslech nemohou číslice opakovat?
Kolik je přirozených dvouciferných čísel, které můžeme utvořit z číslic 0, 1, 2, 3, pokud se v těchto číslech nemohou číslice opakovat? - Můj jediný
 Můj jediný syn se narodil když mi bylo 37 let. to bylo právě 32 let po smrti dědečka a ten zemřel ve svých 64 letech. Dedecek byl o 12 let starší než babička, brali se v roce 1947 právě když babičce bylo 18 let. V kterém roce se narodil můj syn?
Můj jediný syn se narodil když mi bylo 37 let. to bylo právě 32 let po smrti dědečka a ten zemřel ve svých 64 letech. Dedecek byl o 12 let starší než babička, brali se v roce 1947 právě když babičce bylo 18 let. V kterém roce se narodil můj syn? - Vodník
 Vodník Kebule nakupoval v rybárně kapitána Nema, kde ceny všeho zboží byli uvedený v celých šupinách. Kdyby Kebule koupil 2 raky, 3 škeble, a 1 štiku, zaplatil by 49 šupin. Pokud by přikoupil ještě 5 řáku, 11 škeblí a 1 štiku, platil by celkem 154 šupin.
Vodník Kebule nakupoval v rybárně kapitána Nema, kde ceny všeho zboží byli uvedený v celých šupinách. Kdyby Kebule koupil 2 raky, 3 škeble, a 1 štiku, zaplatil by 49 šupin. Pokud by přikoupil ještě 5 řáku, 11 škeblí a 1 štiku, platil by celkem 154 šupin. - DĚTI MO Z6 2021
 Součin věků všech dětí pana Násobka je 1408. Věk nejmladšího dítěte je roven polovině věku nejstaršího dítěte. Kolik dětí má pan Násobek a kolik je jim let?
Součin věků všech dětí pana Násobka je 1408. Věk nejmladšího dítěte je roven polovině věku nejstaršího dítěte. Kolik dětí má pan Násobek a kolik je jim let? - Vierka 3 MO Z8
 Vierka ze tří daných číslic sestavovala navzájem různá trojmístné čísla. Když všechna tato čísla sečetla, vyšlo jí 1221. Jaké číslice Vierka použila? Určete pět možností
Vierka ze tří daných číslic sestavovala navzájem různá trojmístné čísla. Když všechna tato čísla sečetla, vyšlo jí 1221. Jaké číslice Vierka použila? Určete pět možností - Z8 MO 2021
 V dané skupině čísel je jedno číslo rovno průměru všech, největší číslo je o 7 větší než průměr, nejmenší je o 7 menší než průměr a většina čísel ze skupiny má podprůměrnou hodnotu. Jaký nejmenší počet čísel může být ve skupině?
V dané skupině čísel je jedno číslo rovno průměru všech, největší číslo je o 7 větší než průměr, nejmenší je o 7 menší než průměr a většina čísel ze skupiny má podprůměrnou hodnotu. Jaký nejmenší počet čísel může být ve skupině? - Trojnožky
 Na nově objevené planetě žijí zvířata, která astronauti pojmenovali podle počtu nohou jednonožky, dvojnožky, trojnožky a tak dále (zvířata bez nohou tam nebyla). Zvířata s lichým počtem nohou mají dvě hlavy, zvířata se sudým počtem nohou mají jednu hlavu.
Na nově objevené planetě žijí zvířata, která astronauti pojmenovali podle počtu nohou jednonožky, dvojnožky, trojnožky a tak dále (zvířata bez nohou tam nebyla). Zvířata s lichým počtem nohou mají dvě hlavy, zvířata se sudým počtem nohou mají jednu hlavu. - 9 z 10 čísel
 Určete počet devítimístných čísel, ve kterých se každá z číslic 0 až 9 vyskytuje nejvíce jednou a v nichž se součty číslic na 1. až 3. místě, na 3. až 5. místě, na 5. až 7. místě a na 7. až 9. místě vždy rovnají 10. Najděte i nejmenší a největší z těchto
Určete počet devítimístných čísel, ve kterých se každá z číslic 0 až 9 vyskytuje nejvíce jednou a v nichž se součty číslic na 1. až 3. místě, na 3. až 5. místě, na 5. až 7. místě a na 7. až 9. místě vždy rovnají 10. Najděte i nejmenší a největší z těchto - MO Z7-II-1 2020
 Na pohádkovém ostrově žijí draci a kyklopové. Všichni draci jsou červení, tříhlaví a dvounozí. Všichni kyklopové jsou hnědí, jednohlaví a dvounozí. Kyklopové mají jedno oko uprostřed čela, draci mají na každé hlavě dvě oči. Dohromady mají kyklopové a drac
Na pohádkovém ostrově žijí draci a kyklopové. Všichni draci jsou červení, tříhlaví a dvounozí. Všichni kyklopové jsou hnědí, jednohlaví a dvounozí. Kyklopové mají jedno oko uprostřed čela, draci mají na každé hlavě dvě oči. Dohromady mají kyklopové a drac - MO Z7–I–6 2021
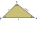 V trojúhelníku ABC leží na straně AC bod D a na straně BC bod E. Velikosti úhlů ABD, BAE, CAE a CBD jsou postupně 30°, 60°, 20° a 30°. určete velikost úhlu AED.
V trojúhelníku ABC leží na straně AC bod D a na straně BC bod E. Velikosti úhlů ABD, BAE, CAE a CBD jsou postupně 30°, 60°, 20° a 30°. určete velikost úhlu AED. - Trojúhelníku 40701
 V trojúhelníku ABC je bod S středem vepsané kružnice. Obsah čtyřúhelníku ABCS je roven čtyřem pětinám obsahu trojúhelníku ABC. Délky stran trojúhelníku ABC vyjádřené v centimetrech jsou všechny celočíselné a obvod trojúhelníku ABC je 15 cm. Určete délky s
V trojúhelníku ABC je bod S středem vepsané kružnice. Obsah čtyřúhelníku ABCS je roven čtyřem pětinám obsahu trojúhelníku ABC. Délky stran trojúhelníku ABC vyjádřené v centimetrech jsou všechny celočíselné a obvod trojúhelníku ABC je 15 cm. Určete délky s - Přístavy MZ
 Mezi přístavy Mumraj a Zmatek pendlují po stejné trase dvě lodě. V přístavech tráví zanedbatelný čas, hned se otáčí a pokračují v plavbě. Ráno ve stejný okamžik vyplouvá modrá loď z přístavu Mumraj a zelená loď z přístavu Zmatek. Poprvé se lodě míjejí 20
Mezi přístavy Mumraj a Zmatek pendlují po stejné trase dvě lodě. V přístavech tráví zanedbatelný čas, hned se otáčí a pokračují v plavbě. Ráno ve stejný okamžik vyplouvá modrá loď z přístavu Mumraj a zelená loď z přístavu Zmatek. Poprvé se lodě míjejí 20
Máš úkol, nad kterým si lámeš alespoň 10 minut hlavu? Pošli nám úkol a my Ti ji zkusíme vypočítat.
