Matematická olympiáda - příklady - strana 6 z 11
Úkoly MO nejsou lehké, ani pro dospělé lidi. Zároveň věříme, že správné řešení, které je zde publikované téměř na jeden klik poslouží jen na inspiraci. V reálném životě každý totiž řeší úkoly, které nikdo jiný před tím neřešil.Nenechte se odradit, když neobjevíte hned řešení. Experimentujte, kreslete si, "hrajte se" s úlohou. Někdy pomůže podívat se do nějaké knížky, kde najdete podobné úkoly vyřešeny, jindy se může stát, že najednou o tři dny "z ničeho nic" na řešení přijdete.
Počet nalezených příkladů: 203
- Z9–I–1 2018 čísla
 Najděte všechna kladná celá čísla x a y, pro která platí: 1/x + 1/y = 1/4
Najděte všechna kladná celá čísla x a y, pro která platí: 1/x + 1/y = 1/4 - Z7-1-3 MO 2018
 Děda připravil pro svých šest vnoučat hromádku lískových oříšků s tím, ať si je nějak rozeberou. První přišel Adam, odpočítal si polovinu, přibral si ještě jeden oříšek a odešel. Stejně se zachoval druhý Bob, třetí Cyril, čtvrtý Dan i pátý Eda. Jen Franta
Děda připravil pro svých šest vnoučat hromádku lískových oříšků s tím, ať si je nějak rozeberou. První přišel Adam, odpočítal si polovinu, přibral si ještě jeden oříšek a odešel. Stejně se zachoval druhý Bob, třetí Cyril, čtvrtý Dan i pátý Eda. Jen Franta - Z9-I-4 2018 Hoteliér
 Hoteliér chtěl vybavit jídelnu novými židlemi. V katalogu si vybral typ židle. Až při zadávání objednávky se od výrobce dozvěděl, že v rámci slevové akce nabízejí každou čtvrtou židli za poloviční cenu a že tedy oproti plánu může ušetřit za sedm a půl žid
Hoteliér chtěl vybavit jídelnu novými židlemi. V katalogu si vybral typ židle. Až při zadávání objednávky se od výrobce dozvěděl, že v rámci slevové akce nabízejí každou čtvrtou židli za poloviční cenu a že tedy oproti plánu může ušetřit za sedm a půl žid - Z9 – I – 2 MO 2018
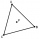 V rovnostranném trojúhelníku ABC je K středem strany AB, bod L leží v třetině strany BC blíže bodu C a bod M leží v třetině strany AC blíže bodu A. Určete, jakou část obsahu trojúhelníku ABC zabírá trojúhelník KLM.
V rovnostranném trojúhelníku ABC je K středem strany AB, bod L leží v třetině strany BC blíže bodu C a bod M leží v třetině strany AC blíže bodu A. Určete, jakou část obsahu trojúhelníku ABC zabírá trojúhelník KLM. - Cifra
 Jaké je poslední číslo 2016-té mocniny čísla 2017?
Jaké je poslední číslo 2016-té mocniny čísla 2017? - Obdélníky 6598
 Adam měl tři shodné obdélníky. Přiložil je k sobě a dostal obdélník s obvodem 50 cm. Potom je přiložil jinak a dostal obdélník s větším obvodem. Vypoctej jeho obvod.
Adam měl tři shodné obdélníky. Přiložil je k sobě a dostal obdélník s obvodem 50 cm. Potom je přiložil jinak a dostal obdélník s větším obvodem. Vypoctej jeho obvod. - Z bodu
 Z bodu A do B je to 16 km z bodu C do B je to 20 km z bodu C do D je to 19 km kolik kilometru to je z bodu D do bodu A
Z bodu A do B je to 16 km z bodu C do B je to 20 km z bodu C do D je to 19 km kolik kilometru to je z bodu D do bodu A - C–I–4 MO 2017
 Určete největší celé číslo n, při kterém lze čtvercovou tabulku n×n zaplnit přirozenými čísly od 1 do n² (n na druhou) tak, aby v každé její čtvercové části 3×3 byla zapsána aspoň jedna druhá mocnina celého čísla.
Určete největší celé číslo n, při kterém lze čtvercovou tabulku n×n zaplnit přirozenými čísly od 1 do n² (n na druhou) tak, aby v každé její čtvercové části 3×3 byla zapsána aspoň jedna druhá mocnina celého čísla. - Rychlostí 5874
 Mišo a Rišo běhali po běžecké dráze tam a zpět. Rozjeli se proti sobě, každý z jiného konce dráhy. Oba stále běželi stejnou rychlostí, každý jinou. Poprvé se setkali 800 m od jednoho konce dráhy, podruhé na druhém konci dráhy. Jakou délku má běžecká dráha
Mišo a Rišo běhali po běžecké dráze tam a zpět. Rozjeli se proti sobě, každý z jiného konce dráhy. Oba stále běželi stejnou rychlostí, každý jinou. Poprvé se setkali 800 m od jednoho konce dráhy, podruhé na druhém konci dráhy. Jakou délku má běžecká dráha - MO Z6-1-3 2017 šachovnica
 Veronika má klasickou šachovnici s 8×8 políčky. Řádky jsou označeny číslicemi 1 až 8, sloupce písmeny A až H. Veronika položila na políčko B1 koně, se kterým lze pohybovat pouze tak jako v šachách. 1. Je možné přemístit koně ve čtyřech tazích na políčko H
Veronika má klasickou šachovnici s 8×8 políčky. Řádky jsou označeny číslicemi 1 až 8, sloupce písmeny A až H. Veronika položila na políčko B1 koně, se kterým lze pohybovat pouze tak jako v šachách. 1. Je možné přemístit koně ve čtyřech tazích na políčko H - Z7-I-5 MO 2017
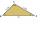 Prokop zostrojil trojuholník ABC, ktorého vnútorný uhol pri vrchole A bol väčší ako 60° a vnútorný uhol pri vrchole B bol menší ako 60°. Juraj narysoval v polrovine určenej priamkou AB a bodom C bod D, a to tak, že trojuholník ABD bol rovnostranný. Potom
Prokop zostrojil trojuholník ABC, ktorého vnútorný uhol pri vrchole A bol väčší ako 60° a vnútorný uhol pri vrchole B bol menší ako 60°. Juraj narysoval v polrovine určenej priamkou AB a bodom C bod D, a to tak, že trojuholník ABD bol rovnostranný. Potom - Z7-1-6 MO 2017
 Vodník Chaluha naléval mlhu do rozmanitých, různě velkých nádob, které si pečlivě seřadil na polici. Při nalévání postupoval postupně z jedné strany, žádnou nádobu nepřeskakoval. Do každé nádoby se vejde alespoň decilitr mlhy. Kdyby naléval mlhu sedmilitr
Vodník Chaluha naléval mlhu do rozmanitých, různě velkých nádob, které si pečlivě seřadil na polici. Při nalévání postupoval postupně z jedné strany, žádnou nádobu nepřeskakoval. Do každé nádoby se vejde alespoň decilitr mlhy. Kdyby naléval mlhu sedmilitr - Z8-I-6 MO 2017
 Přímka představuje číselnou osu a vyznačené body odpovídají číslům a, - a, a + 1, avšak v neurčeném pořadí. Sestrojte body, které odpovídají číslům 0 a 1. Proberte všechny možnosti.
Přímka představuje číselnou osu a vyznačené body odpovídají číslům a, - a, a + 1, avšak v neurčeném pořadí. Sestrojte body, které odpovídají číslům 0 a 1. Proberte všechny možnosti. - Z9-I-6 MO 2017
 Na přímce představující číselnou osu uvažte navzájem různé body odpovídající číslům a, 2a, 3a+1 ve všech možných pořadích. U každé možnosti rozhodněte, zda je takové uspořádání možné. Pokud ano, uveďte konkrétní příklad, pokud ne, zdůvodněte proč.
Na přímce představující číselnou osu uvažte navzájem různé body odpovídající číslům a, 2a, 3a+1 ve všech možných pořadích. U každé možnosti rozhodněte, zda je takové uspořádání možné. Pokud ano, uveďte konkrétní příklad, pokud ne, zdůvodněte proč. - Z5–I–6 MO 2017
 Na stole leželo osm kartiček s čísly 2, 3, 5, 7, 11, 13, 17, 19. Ferda si vybral tři kartičky. Sečetl na nich napsaná čísla a zjistil, že jejich součet je o 1 větší než součet čísel na zbylých kartičkách. Které kartičky mohly zůstat na stole? Určete všech
Na stole leželo osm kartiček s čísly 2, 3, 5, 7, 11, 13, 17, 19. Ferda si vybral tři kartičky. Sečetl na nich napsaná čísla a zjistil, že jejich součet je o 1 větší než součet čísel na zbylých kartičkách. Které kartičky mohly zůstat na stole? Určete všech - Z7-I-4 MO 2017
 Na stole leželo šest kartiček s ciframi 1, 2, 3, 4, 5, 6. Anežka z těchto kartiček složila šestimístné číslo, které bylo dělitelné šesti. Potom postupně odebírala kartičky zprava. Když odebrala první kartičku, zůstalo na stole pětimístné číslo dělitelné p
Na stole leželo šest kartiček s ciframi 1, 2, 3, 4, 5, 6. Anežka z těchto kartiček složila šestimístné číslo, které bylo dělitelné šesti. Potom postupně odebírala kartičky zprava. Když odebrala první kartičku, zůstalo na stole pětimístné číslo dělitelné p - Z9-I-5 MO 2017 obdélník
 Uvnitř obdélníku ABCD leží body E a F tak, že úsečky EA, ED, EF, FB, FC jsou navzájem shodné. Strana AB je dlouhá 22 cm a kružnice opsaná trojúhelníku AFD má poloměr 10cm. Určete délku strany BC.
Uvnitř obdélníku ABCD leží body E a F tak, že úsečky EA, ED, EF, FB, FC jsou navzájem shodné. Strana AB je dlouhá 22 cm a kružnice opsaná trojúhelníku AFD má poloměr 10cm. Určete délku strany BC. - Z9–I–4 MO 2017
 Čísla 1, 2, 3, 4, 5, 6, 7, 8 a 9 se chystala na cestu vlakem se třemi vagóny. Chtěla se rozsadit tak, aby v každém vagóně seděla tři čísla a největší z každé trojice bylo rovno součtu zbylých dvou. Průvodčí tvrdil, že to není problém, a snažil se číslům p
Čísla 1, 2, 3, 4, 5, 6, 7, 8 a 9 se chystala na cestu vlakem se třemi vagóny. Chtěla se rozsadit tak, aby v každém vagóně seděla tři čísla a největší z každé trojice bylo rovno součtu zbylých dvou. Průvodčí tvrdil, že to není problém, a snažil se číslům p - Bonbóny MO Z6-I-5 2017
 V plechovce byly červené a zelené bonbóny. Čeněk snědl 2/5 všech červených bonbónů a Zuzka snědla 3/5 všech zelených bonbónů. Teď tvoří červené bonbóny 3/8 všech bonbónů v plechovce. Kolik nejméně bonbónů mohlo být původně v plechovce?
V plechovce byly červené a zelené bonbóny. Čeněk snědl 2/5 všech červených bonbónů a Zuzka snědla 3/5 všech zelených bonbónů. Teď tvoří červené bonbóny 3/8 všech bonbónů v plechovce. Kolik nejméně bonbónů mohlo být původně v plechovce? - MO Z6 I-3 2017 sklenice
 Honza měl 100 stejných zavařovacích sklenic, z kterých si stavěl trojboké pyramidy. Nejvyšší poschodí pyramidy má vždy jednu sklenici, druhé poschodí shora představuje rovnostranný trojúhelník, jehož strana sestává ze dvou sklenic, atd. Příklad konstrukce
Honza měl 100 stejných zavařovacích sklenic, z kterých si stavěl trojboké pyramidy. Nejvyšší poschodí pyramidy má vždy jednu sklenici, druhé poschodí shora představuje rovnostranný trojúhelník, jehož strana sestává ze dvou sklenic, atd. Příklad konstrukce
Máš úkol, nad kterým si lámeš alespoň 10 minut hlavu? Pošli nám úkol a my Ti ji zkusíme vypočítat.
