Ročník - slovní úlohy a příklady - strana 95 z 743
Počet nalezených příkladů: 14844
- Předpokládejme 75104
 Tři přátelé si rozdělili částku v poměru 2/3: 3/5: 1/4. Předpokládejme, že největší podíl byl 12000,00. Kolik se mezi nimi rozdělilo?
Tři přátelé si rozdělili částku v poměru 2/3: 3/5: 1/4. Předpokládejme, že největší podíl byl 12000,00. Kolik se mezi nimi rozdělilo? - Uspořádaném 75074
 Skóre 10 studentů v testu uspořádaném vzestupně je 12, 13, 13, a, (a + 3), (52 - 2a), (2a - 8), 23, 23 a 24. Pokud je medián 20, najděte (a) hodnotu a. (b) průměr
Skóre 10 studentů v testu uspořádaném vzestupně je 12, 13, 13, a, (a + 3), (52 - 2a), (2a - 8), 23, 23 a 24. Pokud je medián 20, najděte (a) hodnotu a. (b) průměr - Zaokrouhlete 75064
 Vzhledem k trojúhelníku ABC, pokud strana b je 31 stop, strana c je 22 stop a úhel A je 47°, najděte stranu a. Zaokrouhlete na jedno desetinné místo.
Vzhledem k trojúhelníku ABC, pokud strana b je 31 stop, strana c je 22 stop a úhel A je 47°, najděte stranu a. Zaokrouhlete na jedno desetinné místo. - Hodnota výrazu
 Vzhledem k tomu, že p = √(mx/t-t² x) Vytvořte x předmět Pokud m = 7, p = -3 a t = 4, najděte hodnotu x
Vzhledem k tomu, že p = √(mx/t-t² x) Vytvořte x předmět Pokud m = 7, p = -3 a t = 4, najděte hodnotu x
- Geometrickou 75034
 Členy 1/64, 1/32, 1/16 tvoří geometrickou posloupnost (GP) Pokud je součet GP (2³6 – 2^-6), najděte počet členů.
Členy 1/64, 1/32, 1/16 tvoří geometrickou posloupnost (GP) Pokud je součet GP (2³6 – 2^-6), najděte počet členů. - Mnohoúhelníky 75024
 Dva pravidelné mnohoúhelníky, x a y, jsou takové, že počet stran x je o tři větší než počet stran y. Pokud je součet vnějších úhlů x a y 117°, kolik stran má x?
Dva pravidelné mnohoúhelníky, x a y, jsou takové, že počet stran x je o tři větší než počet stran y. Pokud je součet vnějších úhlů x a y 117°, kolik stran má x? - Čtverečních 75014
 Povrch krychle je roven 294 metrů čtverečních. Vypočtěte hranu a objem krychle.
Povrch krychle je roven 294 metrů čtverečních. Vypočtěte hranu a objem krychle. - Odpoledne 75004
 Josef koupí 120 trsů narcisů spolu za 80 liber a 80 trsů tulipánů spolu za 50 liber. Josef pak prodává květiny na trhu. Ráno Josef prodá 75 svazků narcisů za svazek 80p a 50 svazků tulipánů za svazek 90p. Odpoledne Josef prodá všechny kytice, které jí zůs
Josef koupí 120 trsů narcisů spolu za 80 liber a 80 trsů tulipánů spolu za 50 liber. Josef pak prodává květiny na trhu. Ráno Josef prodá 75 svazků narcisů za svazek 80p a 50 svazků tulipánů za svazek 90p. Odpoledne Josef prodá všechny kytice, které jí zůs - 4místných 74994
 Vzhledem k číslicím 0-7. Pokud opakování není povoleno, kolik 4místných kódů, které jsou větší než 2000 a dělitelné 4, je možných?
Vzhledem k číslicím 0-7. Pokud opakování není povoleno, kolik 4místných kódů, které jsou větší než 2000 a dělitelné 4, je možných?
- Diferencovatelné 74984
 A). Načrtněte graf funkce f(x)=x * abs(x) = x * |x| b). Pro jaké hodnoty x je f(x) diferencovatelné c). Najít F(x)
A). Načrtněte graf funkce f(x)=x * abs(x) = x * |x| b). Pro jaké hodnoty x je f(x) diferencovatelné c). Najít F(x) - Trojúhelníku 74914
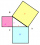 Urči obvod trojúhelníku ABC kde bod A je začátek souřadnicové soustavy, bod B je průsečík grafu linearní funkce f: y = - 3/4• x + 3 s osou x a C je průsečík grafu této funkce s osou y.
Urči obvod trojúhelníku ABC kde bod A je začátek souřadnicové soustavy, bod B je průsečík grafu linearní funkce f: y = - 3/4• x + 3 s osou x a C je průsečík grafu této funkce s osou y. - Předpokládal 74894
 Pan Gábor vydělává čtvrtletně 12 %. Předpokládal, že po deseti letech vysbírá 500 000 pesos. Jakou částku musí investovat?
Pan Gábor vydělává čtvrtletně 12 %. Předpokládal, že po deseti letech vysbírá 500 000 pesos. Jakou částku musí investovat? - Souřadnice 74874
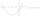 Rovnice křivky C je y = 2x2 - 8x +9 a rovnice přímky L je x + y = 3. (1) Najděte x-ové souřadnice průsečíků L a C. ii) ukázat, že jeden z těchto bodů je také
Rovnice křivky C je y = 2x2 - 8x +9 a rovnice přímky L je x + y = 3. (1) Najděte x-ové souřadnice průsečíků L a C. ii) ukázat, že jeden z těchto bodů je také - Motorového 74864
 Rychlostní člun ujede 900 km proti proudu 25 km/h. Cesta mu trvala o 10 minut déle, než by trvala cesta proudem. Jaká je rychlost motorového člunu na stojaté vodě?
Rychlostní člun ujede 900 km proti proudu 25 km/h. Cesta mu trvala o 10 minut déle, než by trvala cesta proudem. Jaká je rychlost motorového člunu na stojaté vodě?
- Obsahuje 74844
 Tyčinka obsahuje na 50 gramů 12 gramů cukru. Kolik procent cukru obsahuje tyčinka?
Tyčinka obsahuje na 50 gramů 12 gramů cukru. Kolik procent cukru obsahuje tyčinka? - Vypočítejte 74834
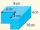 Z jednoho rohu původního kvádru se podle obrázku vyřízne kvádr o hloubce 4 cm, ale délce a šířce x cm (původní kvádr má rozměry 10x8x4 cm). Zbývající tvar má objem 199. Vypočítejte hodnotu x.
Z jednoho rohu původního kvádru se podle obrázku vyřízne kvádr o hloubce 4 cm, ale délce a šířce x cm (původní kvádr má rozměry 10x8x4 cm). Zbývající tvar má objem 199. Vypočítejte hodnotu x. - Vzdáleny 74804
 Najděte rovnici pro všechny body (x,y), které jsou rovněž vzdáleny od bodů A(5,-2) a B(-2,10)?
Najděte rovnici pro všechny body (x,y), které jsou rovněž vzdáleny od bodů A(5,-2) a B(-2,10)? - Matematiky 74794
 Dřevěný válec o průměru 20cm a délce 1m je ponořený do vody. Měrná hmotnost dřeva je 700kg/m³. Třeba vypočítat výšku dřeva, který je nad vodou. Role mi byla zadána jako vstupní písemka z matematiky pro prvňáka na střední škole před 52. lety
Dřevěný válec o průměru 20cm a délce 1m je ponořený do vody. Měrná hmotnost dřeva je 700kg/m³. Třeba vypočítat výšku dřeva, který je nad vodou. Role mi byla zadána jako vstupní písemka z matematiky pro prvňáka na střední škole před 52. lety - Nejmenší 74784
 Najděte nejmenší společný násobek 4x³ + 8x² a 5x² -20
Najděte nejmenší společný násobek 4x³ + 8x² a 5x² -20
Máš úkol, nad kterým si lámeš alespoň 10 minut hlavu? Pošli nám úkol a my Ti ji zkusíme vypočítat.
