Vektor - příklady
Pokyny: Vyřešte každý úkol pečlivě a ukažte své celé řešení. Pokud je to vhodné, proveďte zkoušku správnosti řešení.Počet nalezených příkladů: 116
- Zatáčka 3
 Zatáčka má poloměr r = 100 m a je sklopena pod úhlem 20° vůči vodorovné rovině (= úhel klopení). Jaká je bezpečná (ta "nejlepší")rychlost při průjezdu touto zatáčkou? Načrtni obrázek z hlediska NIVS, vyznač síly a vypočítej.
Zatáčka má poloměr r = 100 m a je sklopena pod úhlem 20° vůči vodorovné rovině (= úhel klopení). Jaká je bezpečná (ta "nejlepší")rychlost při průjezdu touto zatáčkou? Načrtni obrázek z hlediska NIVS, vyznač síly a vypočítej. - Soňa sedí
 Soňa sedí ve vlaku, dívá se z okýnka a co nevidí: krajina ubíhá dozadu stálou rychlostí 160 km/h a na vedlejší koleji zdánlivě couvá vlak stálou rychlostí 40km/h. Soňa se zarazí a chvilku přemýšlí, kterým směrem a jak rychle druhý vlak ve skutečnosti jede
Soňa sedí ve vlaku, dívá se z okýnka a co nevidí: krajina ubíhá dozadu stálou rychlostí 160 km/h a na vedlejší koleji zdánlivě couvá vlak stálou rychlostí 40km/h. Soňa se zarazí a chvilku přemýšlí, kterým směrem a jak rychle druhý vlak ve skutečnosti jede - Ortocentrum
 Je dán trojúhelník ABC: A (-1,3), B(2,-2), C(-4,-3). Urči souřadnice průsečíku výšek a souřadnice průsečík os stran.
Je dán trojúhelník ABC: A (-1,3), B(2,-2), C(-4,-3). Urči souřadnice průsečíku výšek a souřadnice průsečík os stran. - Operace 4
 Operace * (hviezdička) přiřazujíci dvěma dvojicím čísel jedno číslo je zavedena takto: (a, b)*(c, d) = ac+bd víme že: (x,2)*(-1, v) = -1 a (2,-1)*(u, v)=5 a (u, v)*(1,1)=-2 Čemu je rovno (1,2)*(x, y) jesliže y=3?
Operace * (hviezdička) přiřazujíci dvěma dvojicím čísel jedno číslo je zavedena takto: (a, b)*(c, d) = ac+bd víme že: (x,2)*(-1, v) = -1 a (2,-1)*(u, v)=5 a (u, v)*(1,1)=-2 Čemu je rovno (1,2)*(x, y) jesliže y=3? - Tři kamarádi 8
 Tři kamarádi sedí na molu, které je přesně uprostřed tekoucí řeky. prvni kamarád se vydává proti proudu řeky rychlostí 0,4 m/s, druhý kamarád se vydává po proudu řeky rychlostí 0,2 m/s, třetí kamarád pluje kolmo směrem ke břehu rychlostí 0,8 m/s. Rychlost
Tři kamarádi sedí na molu, které je přesně uprostřed tekoucí řeky. prvni kamarád se vydává proti proudu řeky rychlostí 0,4 m/s, druhý kamarád se vydává po proudu řeky rychlostí 0,2 m/s, třetí kamarád pluje kolmo směrem ke břehu rychlostí 0,8 m/s. Rychlost - Vzdálenost 83160
 Vypočítej vzdálenost bodu A[ 4; 2; -3 ] od roviny : 2x - 2y + z + 5 = 0
Vypočítej vzdálenost bodu A[ 4; 2; -3 ] od roviny : 2x - 2y + z + 5 = 0 - Konjugát 83061
 Tři vektory A, B a C souvisí takto: A/C = 2 při 120 stupních, A + B = -5 + j15, C = konjugát B. Najděte C.
Tři vektory A, B a C souvisí takto: A/C = 2 při 120 stupních, A + B = -5 + j15, C = konjugát B. Najděte C. - Vypočítejte 82992
 Je dán kvádr ABCDEFGH. Víme, že |AB| = 1 cm, |BC| = 2 cm, |AE| = 3 cm. Vypočítejte ve stupních velikost úhlu, který svírají přímky BG a FH .
Je dán kvádr ABCDEFGH. Víme, že |AB| = 1 cm, |BC| = 2 cm, |AE| = 3 cm. Vypočítejte ve stupních velikost úhlu, který svírají přímky BG a FH . - Zemní rychlost
 Letadlo letí na jih průměrnou rychlostí 190km/h, od západu na východ fuka vítr rychlostí 20m/s . Jak rychle a jakým směrem (vzhledem k poledníku) se bude letadlo přemísťovat vzhledem k zemi?
Letadlo letí na jih průměrnou rychlostí 190km/h, od západu na východ fuka vítr rychlostí 20m/s . Jak rychle a jakým směrem (vzhledem k poledníku) se bude letadlo přemísťovat vzhledem k zemi? - Vektory 82034
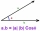 Dány jsou vektory a = (3, -2), b = (-1, 5). Určete vektor c, pro který platí a. c = 17; c = 3
Dány jsou vektory a = (3, -2), b = (-1, 5). Určete vektor c, pro který platí a. c = 17; c = 3 - Velikostmi 81758
 Sílu velikosti F = 100 N rozložte na dvě kolmé složky s velikostmi F1, F2 tak, aby úhel mezi silami F1 a F byl 43°52'.
Sílu velikosti F = 100 N rozložte na dvě kolmé složky s velikostmi F1, F2 tak, aby úhel mezi silami F1 a F byl 43°52'. - Souřadnicích 80975
 Trojúhelník PQR má vrcholy umístěné na souřadnicích (2, 2), (5, -4) a (-4, -1). Jaký typ trojúhelníku je trojúhelník PQR?
Trojúhelník PQR má vrcholy umístěné na souřadnicích (2, 2), (5, -4) a (-4, -1). Jaký typ trojúhelníku je trojúhelník PQR? - Rychlostí 79534
 Letadlo se pohybuje ve směru 45 stupňů severní šířky východu rychlostí 320 km/h, když narazí na proud z východu na jihu o rychlosti 115 stupňů 20 km/h. Jaký je nový kurz a rychlost letadla?
Letadlo se pohybuje ve směru 45 stupňů severní šířky východu rychlostí 320 km/h, když narazí na proud z východu na jihu o rychlosti 115 stupňů 20 km/h. Jaký je nový kurz a rychlost letadla? - PQ=4*vektor 78264
 PQRS je čtyřúhelník s P(4,4), S(8,8) a R(12,8). Pokud vektor PQ=4*vektor SR, najděte souřadnice Q. Vyřešte to
PQRS je čtyřúhelník s P(4,4), S(8,8) a R(12,8). Pokud vektor PQ=4*vektor SR, najděte souřadnice Q. Vyřešte to - Zaokrouhlete 72864
 Muž, který se toulá pouští, ujede 3,8 míle ve směru S 44° W západní délky. Potom se otočí a ujede 2,2 míle ve směru severní N 55° W západní délky. Jak daleko je v té době od svého výchozího bodu? (Vaši odpověď zaokrouhlete na dvě desetinná místa.)
Muž, který se toulá pouští, ujede 3,8 míle ve směru S 44° W západní délky. Potom se otočí a ujede 2,2 míle ve směru severní N 55° W západní délky. Jak daleko je v té době od svého výchozího bodu? (Vaši odpověď zaokrouhlete na dvě desetinná místa.) - Vzdálenost 71874
 Hlídka měla určený pochodový úhel 13°. Po ujetí 9 km se úhel změnil na 62°. Tímto směrem šla hlídka 10 km. zjistí vzdálenost od místa, ze kterého hlídka vyšla.
Hlídka měla určený pochodový úhel 13°. Po ujetí 9 km se úhel změnil na 62°. Tímto směrem šla hlídka 10 km. zjistí vzdálenost od místa, ze kterého hlídka vyšla. - Síla R
 Síla R = 12 N se má rozdělit na dvě složky F1, F2, jejich směry svírají se směrem síly R úhly α = 30°, β = 45°. Jaké jsou složky F1, F2?
Síla R = 12 N se má rozdělit na dvě složky F1, F2, jejich směry svírají se směrem síly R úhly α = 30°, β = 45°. Jaké jsou složky F1, F2? - Vypočítejte 198
 Vypočítejte obsah a obvod pravoúhlého trojúhelníku ABC, je-li A[5,5;-2,5] B[-3;5] C[-3;-2,5]
Vypočítejte obsah a obvod pravoúhlého trojúhelníku ABC, je-li A[5,5;-2,5] B[-3;5] C[-3;-2,5] - Katka 6
 Katka a Honza vyjeli na koloběžkách ve stejnou dobu. Katka jela rychlostí 4,5 km/30 min a Honza jel rychlostí 4km/20 min. a) kolik m ujeli za 2 min když jeli opačným směrem? b) kolik m ujeli když Honza jel směrem na severovýchod a Katka směrem na jihových
Katka a Honza vyjeli na koloběžkách ve stejnou dobu. Katka jela rychlostí 4,5 km/30 min a Honza jel rychlostí 4km/20 min. a) kolik m ujeli za 2 min když jeli opačným směrem? b) kolik m ujeli když Honza jel směrem na severovýchod a Katka směrem na jihových - Pohybovalo 62844
 Těleso o hmotnosti 4 kg narazilo na překážku rychlostí 10 m/s. Po srážce se těleso dále pohybovalo rychlostí 6 m/s, přičemž směr této rychlosti byl kolmý na směr rychlosti před srážkou. Určete a) změnu velikosti rychlosti a hybnosti tělesa a b) velikost z
Těleso o hmotnosti 4 kg narazilo na překážku rychlostí 10 m/s. Po srážce se těleso dále pohybovalo rychlostí 6 m/s, přičemž směr této rychlosti byl kolmý na směr rychlosti před srážkou. Určete a) změnu velikosti rychlosti a hybnosti tělesa a b) velikost z
Máš úkol, nad kterým si lámeš alespoň 10 minut hlavu? Pošli nám úkol a my Ti ji zkusíme vypočítat.
