Povrch tělesa + vyjádření neznámé ze vzorce - příklady a úlohy
Počet nalezených příkladů: 368
- Věžička 2
 Věžička má půdorys tvaru čtverce s délkou strany 5m. Střecha věžičky má tvar pravidelného čtyřbokého jehlanu (bez podstavy) s výškou 8m. Při rekonstrukci se bude střecha pokrývat novými taškami. Na 1 m² se spotřebuje 11 tašek. Na jedné paletě je uskladněn
Věžička má půdorys tvaru čtverce s délkou strany 5m. Střecha věžičky má tvar pravidelného čtyřbokého jehlanu (bez podstavy) s výškou 8m. Při rekonstrukci se bude střecha pokrývat novými taškami. Na 1 m² se spotřebuje 11 tašek. Na jedné paletě je uskladněn - Obvod 34
 Obvod podstavy pravidelného čtyřbokého jehlanu je stejně velký jako jeho výška. Jehlan má objem 288 dm³. Vypočítejte jeho povrch. Výsledek zaokrouhlete na celé dm².
Obvod podstavy pravidelného čtyřbokého jehlanu je stejně velký jako jeho výška. Jehlan má objem 288 dm³. Vypočítejte jeho povrch. Výsledek zaokrouhlete na celé dm². - Osový řez válce
 Osovým řezem válce je čtverec o obsahu 56,25 cm². Vypočítejte jeho povrch a objem. Výsledek vyjádřete ve čtverečných decimetrech a v krychlových decimetrech a zaokrouhlete na setiny.
Osovým řezem válce je čtverec o obsahu 56,25 cm². Vypočítejte jeho povrch a objem. Výsledek vyjádřete ve čtverečných decimetrech a v krychlových decimetrech a zaokrouhlete na setiny. - Povrch 32
 Povrch rotačního kužele a obsah jeho podstavy jsou v poměru 18:5. Určete objem kužele, je-li jeho tělesná výška 12 cm.
Povrch rotačního kužele a obsah jeho podstavy jsou v poměru 18:5. Určete objem kužele, je-li jeho tělesná výška 12 cm.
- Papírová
 Papírová krabice má tvar krychle. Na její výrobu bylo spotřebováno 2400 cm².Ohyby pro přilepení stěn se nezapočítávají. Jaký je objem krabice?
Papírová krabice má tvar krychle. Na její výrobu bylo spotřebováno 2400 cm².Ohyby pro přilepení stěn se nezapočítávají. Jaký je objem krabice? - Objem 30
 Objem kvádru je 960 cm³. Délky hran jsou v poměru 1 : 3 : 5. Vypočtěte povrch kvádru.
Objem kvádru je 960 cm³. Délky hran jsou v poměru 1 : 3 : 5. Vypočtěte povrch kvádru. - Kulová úseč 4
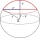 Vypočítejte objem kulové úseče a povrch vrchlíku. Je-li poloměr koule r=5cm a poloměr kruhové podstavy úseče ρ=4cm.
Vypočítejte objem kulové úseče a povrch vrchlíku. Je-li poloměr koule r=5cm a poloměr kruhové podstavy úseče ρ=4cm. - Povrch 33
 Povrch kvádru je 5 632 m². Délky hran jsou v poměru 1 : 2 : 3. Vypočtěte objem kvádru.
Povrch kvádru je 5 632 m². Délky hran jsou v poměru 1 : 2 : 3. Vypočtěte objem kvádru. - Objem 31
 Objem kvádru je 7 500 dm³. Délky hran jsou v poměru 3 : 4 : 5. Vypočtěte povrch kvádru.
Objem kvádru je 7 500 dm³. Délky hran jsou v poměru 3 : 4 : 5. Vypočtěte povrch kvádru.
- Je dán 25
 Je dán rotační kužel s výškou 18 cm a délkou boční strany s = 45 cm. Vypočtěte povrch a objem
Je dán rotační kužel s výškou 18 cm a délkou boční strany s = 45 cm. Vypočtěte povrch a objem - Válec 27
 Válec má stejný průměr jako výšku. Vypočítejte tyto údaje. je-li povrch 200 cm čtverečních. Výsledky uveďte s přesností na milimetry
Válec má stejný průměr jako výšku. Vypočítejte tyto údaje. je-li povrch 200 cm čtverečních. Výsledky uveďte s přesností na milimetry - Válec 28
 Válec má povrch pláště 88 cm čtverečních a objem 176 cm krychlových. Vypočítejte poloměr, výšku a povrch uvedeného tělesa
Válec má povrch pláště 88 cm čtverečních a objem 176 cm krychlových. Vypočítejte poloměr, výšku a povrch uvedeného tělesa - Spádnice
 Určit objem a povrch kužele, jehož spádnice o délce 8cm svírá s rovinou podstavy úhel 75 stupňů
Určit objem a povrch kužele, jehož spádnice o délce 8cm svírá s rovinou podstavy úhel 75 stupňů - Z povrchu objem
 Povrch kužele je 75,36 cm, poloměr je 3cm. Vypočítej objem kužele.
Povrch kužele je 75,36 cm, poloměr je 3cm. Vypočítej objem kužele.
- Objem 32
 Objem krychle je 0,512 m³. Vypočtěte její povrch.
Objem krychle je 0,512 m³. Vypočtěte její povrch. - Valec obecne
 Jak vysoký je válec, jehož plášť má obsah rovný obsahu podstavy? Jaká je objem tohoto válce?
Jak vysoký je válec, jehož plášť má obsah rovný obsahu podstavy? Jaká je objem tohoto válce? - Povrch 34
 Povrch krychle je 150 dm². Vypočtěte její objem.
Povrch krychle je 150 dm². Vypočtěte její objem. - Prosím 6
 Prosím o vyjádření r ze vzorce pro povrch válce.
Prosím o vyjádření r ze vzorce pro povrch válce. - Hrana krychle 3
 Hrana krychle má délku a=1. Určete délku hrany krychle, která má dvojnásobný povrch.
Hrana krychle má délku a=1. Určete délku hrany krychle, která má dvojnásobný povrch.
Máš úkol, nad kterým si lámeš alespoň 10 minut hlavu? Pošli nám úkol a my Ti ji zkusíme vypočítat.
