Pětiúhelník
Uvnitř pravidelného pětiúhelníku ABCDE je bod P takový, že trojúhelník ABP je rovnostranný. Jak velký je úhel BCP?
Udělej si náčrtek
Udělej si náčrtek
Správná odpověď:
Zobrazuji 5 komentářů:
Žák
trojuhelnik abp jr rovnostranny dle zadani,proto strana ab=bp=pa.u petiuhelniku ab=bc=bp. trojuhelnik bcp je rovnoramenny,,bc=bp. vsechny uhly petiuhelniku =360 st. uhel abc=360;5=72st. rovnostranny trojuhelnik ma wsoucet180st.pokud uhel abc=72st.,uhelpbc=72-60=12st. Trojuhelnik pbc je rovnoramenny pb=bc. Uhel bcp a cpb=180-12=168st. Uhel bcp=168;2=84st
Mo - Oficiální
Nápověda. Uvědomte si, že trojúhelník BCP není obecný.
Možné řešení. Pětiúhelník ABCDE je pravidelný, zejména platí |AB| = |BC|. Trojúhelník ABP je rovnostranný, zejména platí |AB| = |BP|. Odtud vidíme, že |BP| = |BC|, tedy, že trojúhelník BCP je rovnoramenný. Jeho vnitřní úhly u vrcholů P a C jsou proto shodné; k jejich určení stačí znát úhel u vrcholu B (součet velikostí vnitřních úhlů v libovolném trojúhelníku je 180◦). Přitom úhel P BC je rozdílem úhlů ABC a ABP, z nichž první je vnitřním úhlem pravidelného pětiúhelníku (vyjádříme záhy) a druhý je vnitřním úhlem rovnostranného trojúhelníku (má velikost α = 60◦).
Pětiúhelník ABCDE můžeme rozdělit na pět trojúhelníků se společným vrcholem P. Součet vnitřních úhlů pětiúhelníku je roven součtu vnitřních úhlů všech pěti trojúhelníků vyjma úhlů u vrcholu P, tj. 5·180◦−360◦ = 540◦. V pravidelném pětiúhelníku jsou všechny vnitřní úhly shodné, každý má tudíž velikost 540◦: 5 = 108◦.
Odtud konečně umíme vyjádřit β = |?P BC| = |?ABC| − |?ABP| = 108◦ − 60◦ = 48◦
a následně γ = |?BCP| = |?BPC| = (180◦ − 48◦)/2 = 66◦.
Velikost úhlu BCP je 66◦.
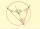
Poznámka. Velikost vnitřního úhlu pravidelného pětiúhelníku je možné odvodit také pomocí rozdělení na pět shodných rovnoramenných trojúhelníků jako na následujícím obrázku (S je střed pětiúhelníku, tj. střed jemu opsané kružnice).
Úhel u vrcholu S v každém z těchto trojúhelníků má velikost 360 : 5 = 72◦; součet úhlů u základny je roven 180◦−72◦ = 108◦ , což je také velikost vnitřního úhlu pravidelného pětiúhelníku.
Možné řešení. Pětiúhelník ABCDE je pravidelný, zejména platí |AB| = |BC|. Trojúhelník ABP je rovnostranný, zejména platí |AB| = |BP|. Odtud vidíme, že |BP| = |BC|, tedy, že trojúhelník BCP je rovnoramenný. Jeho vnitřní úhly u vrcholů P a C jsou proto shodné; k jejich určení stačí znát úhel u vrcholu B (součet velikostí vnitřních úhlů v libovolném trojúhelníku je 180◦). Přitom úhel P BC je rozdílem úhlů ABC a ABP, z nichž první je vnitřním úhlem pravidelného pětiúhelníku (vyjádříme záhy) a druhý je vnitřním úhlem rovnostranného trojúhelníku (má velikost α = 60◦).
Pětiúhelník ABCDE můžeme rozdělit na pět trojúhelníků se společným vrcholem P. Součet vnitřních úhlů pětiúhelníku je roven součtu vnitřních úhlů všech pěti trojúhelníků vyjma úhlů u vrcholu P, tj. 5·180◦−360◦ = 540◦. V pravidelném pětiúhelníku jsou všechny vnitřní úhly shodné, každý má tudíž velikost 540◦: 5 = 108◦.
Odtud konečně umíme vyjádřit β = |?P BC| = |?ABC| − |?ABP| = 108◦ − 60◦ = 48◦
a následně γ = |?BCP| = |?BPC| = (180◦ − 48◦)/2 = 66◦.
Velikost úhlu BCP je 66◦.
Poznámka. Velikost vnitřního úhlu pravidelného pětiúhelníku je možné odvodit také pomocí rozdělení na pět shodných rovnoramenných trojúhelníků jako na následujícím obrázku (S je střed pětiúhelníku, tj. střed jemu opsané kružnice).
Úhel u vrcholu S v každém z těchto trojúhelníků má velikost 360 : 5 = 72◦; součet úhlů u základny je roven 180◦−72◦ = 108◦ , což je také velikost vnitřního úhlu pravidelného pětiúhelníku.
8 let 1 Like
Tipy na související online kalkulačky
Vypočet rovnostranného trojúhelníku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Jednotky fyzikálních veličin:
Téma:
Úroveň náročnosti úkolu:
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Pětiúhelník
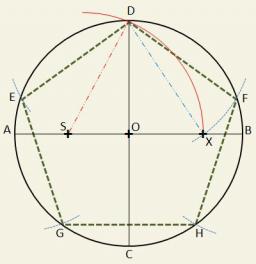
 Vývěsní štít má tvar pětiúhelníku ABCDE, ve kterém úsečka BC je kolmá na úsečku AB a EA je kolmá na úsečku AB. Bod P je pata kolmice spuštění z bodu D na úsečku AB. |AP|=|PB|, |BC|=|EA|=6dm, |PD|=8,4dm. Na štítu je vyznačen bod X - průsečík úseček PE a DA
Vývěsní štít má tvar pětiúhelníku ABCDE, ve kterém úsečka BC je kolmá na úsečku AB a EA je kolmá na úsečku AB. Bod P je pata kolmice spuštění z bodu D na úsečku AB. |AP|=|PB|, |BC|=|EA|=6dm, |PD|=8,4dm. Na štítu je vyznačen bod X - průsečík úseček PE a DA - Vypočítej 80
 Vypočítej, vejde-li se obdélníkový obraz s rozměry 33cm a 70cm do kufru s rozměry 65cm, 40cm a 20cm. Udělej si náčrtek, zapiš jako slovní úlohu.
Vypočítej, vejde-li se obdélníkový obraz s rozměry 33cm a 70cm do kufru s rozměry 65cm, 40cm a 20cm. Udělej si náčrtek, zapiš jako slovní úlohu. - Půlkruh
 V půlkruhu se středem S a průměrem AB je sestrojen rovnostranný trojúhelník SBC. Jaká je velikost úhlu ∠ SAC?
V půlkruhu se středem S a průměrem AB je sestrojen rovnostranný trojúhelník SBC. Jaká je velikost úhlu ∠ SAC? - Obdélník JANO
 Obdélník má délky stran | JA | = 16cm a | AN | = 12cm. Bod S je střed strany JO a bod T je střed strany JA. Vypočítejte obvod pětiúhelníku v cm.
Obdélník má délky stran | JA | = 16cm a | AN | = 12cm. Bod S je střed strany JO a bod T je střed strany JA. Vypočítejte obvod pětiúhelníku v cm.
- Vypočítejte 7
 Vypočítejte délku úhlopříčky pravidelného pětiúhelníku: a) vepsaného do kružnice o poloměru 12dm; b) opsaného kružnici o poloměru 12dm.
Vypočítejte délku úhlopříčky pravidelného pětiúhelníku: a) vepsaného do kružnice o poloměru 12dm; b) opsaného kružnici o poloměru 12dm. - 5 - úhelník
 Vypočítejte délku strany a, obvod a obsah pravidelného pětiúhelníku, který je vepsán do kružnice o poloměru r=6 cm.
Vypočítejte délku strany a, obvod a obsah pravidelného pětiúhelníku, který je vepsán do kružnice o poloměru r=6 cm. - Obsah pětiúhelníku
 Vypočítejte obsah pravidelného pětiúhelníku se stranou 31 cm.
Vypočítejte obsah pravidelného pětiúhelníku se stranou 31 cm. - Rovnoramenný 2588
 Daný je rovnoramenný lichoběžník ABCD, ve kterém platí |AB|= 2|BC|= 2|CD|= 2|DA|. Na jeho straně BC je bod K takový, že |BK| = 2|KC|, na jeho straně CD je bod L takový, že |CL|= 2|LD|, a na jeho straně DA je bod M takový, že|DM|= 2|MA|. Určete velikosti v
Daný je rovnoramenný lichoběžník ABCD, ve kterém platí |AB|= 2|BC|= 2|CD|= 2|DA|. Na jeho straně BC je bod K takový, že |BK| = 2|KC|, na jeho straně CD je bod L takový, že |CL|= 2|LD|, a na jeho straně DA je bod M takový, že|DM|= 2|MA|. Určete velikosti v - Je dána 2
 Je dána kružnice s poloměrem 2,5 cm a bod A, který na ni leží. Do kružnice vepište rovnostranný trojúhelník ABC.
Je dána kružnice s poloměrem 2,5 cm a bod A, který na ni leží. Do kružnice vepište rovnostranný trojúhelník ABC.
- Rovnostranný 7962
 Po dlouhém večeři uvnitř salonku ve tvaru čtverce ABCD leží opilý kupec E tak, že trojúhelník DEC je rovnostranný. Na hraně BC leží špeh F, přičemž |EB|=|EF|. Jaká je velikost úhlu CEF?
Po dlouhém večeři uvnitř salonku ve tvaru čtverce ABCD leží opilý kupec E tak, že trojúhelník DEC je rovnostranný. Na hraně BC leží špeh F, přičemž |EB|=|EF|. Jaká je velikost úhlu CEF? - Šestiúhelník a rovnostranný △
 Obvod rovnostranného △ PQR je 12. Obvod pravidelného šestiúhelníku STUVWX je také 12. Jaký je poměr plochy △ PQR k oblasti STUVWX?
Obvod rovnostranného △ PQR je 12. Obvod pravidelného šestiúhelníku STUVWX je také 12. Jaký je poměr plochy △ PQR k oblasti STUVWX? - Pětiúhelník
 Vypočítejte obsah pravidelného pětiúhelníku, jehož úhlopříčka je dlouhá u=20.
Vypočítejte obsah pravidelného pětiúhelníku, jehož úhlopříčka je dlouhá u=20. - Stoupání 30241
 Rovná cesta má stoupání 19%. Jak velký je úhel stoupání?
Rovná cesta má stoupání 19%. Jak velký je úhel stoupání? - Čtyřúhelníku 82395
 Body ABC leží na kružnici k(S, r) tak, že úhel u B je tupý. Jak velký musí být úhel u vrcholu B čtyřúhelníku SCBA, aby byl tento úhel třikrát větší než vnitřní úhel ASC téhož čtyřúhelníku?
Body ABC leží na kružnici k(S, r) tak, že úhel u B je tupý. Jak velký musí být úhel u vrcholu B čtyřúhelníku SCBA, aby byl tento úhel třikrát větší než vnitřní úhel ASC téhož čtyřúhelníku?
- Stoupání
 Cesta má stoupání 1:18. Jak velký úhel odpovídá takovému stoupání?
Cesta má stoupání 1:18. Jak velký úhel odpovídá takovému stoupání? - Úhly v trojúhelníku 2
 V trojúhelníku ABC je vnitřní úhel při vrcholu C dvakrát větší než vnitřní úhel při vrcholu A. Vnější úhel při vrcholu B měří 117°. Jak velký je vnější úhel při vrcholu A?
V trojúhelníku ABC je vnitřní úhel při vrcholu C dvakrát větší než vnitřní úhel při vrcholu A. Vnější úhel při vrcholu B měří 117°. Jak velký je vnější úhel při vrcholu A? - Z9-I-5 MO 2017 obdélník
 Uvnitř obdélníku ABCD leží body E a F tak, že úsečky EA, ED, EF, FB, FC jsou navzájem shodné. Strana AB je dlouhá 22 cm a kružnice opsaná trojúhelníku AFD má poloměr 10cm. Určete délku strany BC.
Uvnitř obdélníku ABCD leží body E a F tak, že úsečky EA, ED, EF, FB, FC jsou navzájem shodné. Strana AB je dlouhá 22 cm a kružnice opsaná trojúhelníku AFD má poloměr 10cm. Určete délku strany BC.
