Kvadratická rovnice
Určitě čísla b, c tak aby čísla x1 = -1 a x2 = 6 byly kořeny kvadratické rovnice:
4x2+bx+c=0
4x2+bx+c=0
Správná odpověď:
Tipy na související online kalkulačky
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Úroveň náročnosti úkolu:
Související a podobné příklady:
- Kořeny
 Určitě v kvadratické rovnici absolutní člen q tak, aby rovnice měla reálný dvojnásobný kořen a tento kořen x vypočítejte: 5x ² +9x + q = 0
Určitě v kvadratické rovnici absolutní člen q tak, aby rovnice měla reálný dvojnásobný kořen a tento kořen x vypočítejte: 5x ² +9x + q = 0 - Součin a součet kořenů
 Najděte součin a součet kořenů kvadratické rovnice x² + 3x - 9 = 0 Aplikujte vztahy mezi kořeny a koeficienty kvadratické rovnice.
Najděte součin a součet kořenů kvadratické rovnice x² + 3x - 9 = 0 Aplikujte vztahy mezi kořeny a koeficienty kvadratické rovnice. - Rovnice 46771
 Mezi kořeny rovnice 4x² - 17x + 4= 0 vložte tři čísla tak, aby tvořily s danými čísly GP
Mezi kořeny rovnice 4x² - 17x + 4= 0 vložte tři čísla tak, aby tvořily s danými čísly GP - Kvadratická rovnice
 Kvadratická rovnice -4x²+bx+c=0 má kořeny x1 = 85 a x2 = -46. Vypočítejte koeficienty b a c.
Kvadratická rovnice -4x²+bx+c=0 má kořeny x1 = 85 a x2 = -46. Vypočítejte koeficienty b a c.
- Stačí dosedit
 Určete kořen kvadratické rovnice: 3x²-4x + (-4) = 0.
Určete kořen kvadratické rovnice: 3x²-4x + (-4) = 0. - Nulové body
 Vypočítejte kořeny rovnice: 1 |x +4| -2 |x -9| +4 |x +3| = 42
Vypočítejte kořeny rovnice: 1 |x +4| -2 |x -9| +4 |x +3| = 42 - Kvadratické funkce
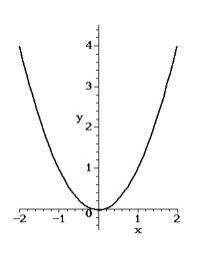
 Y=x²+4x-2 Kvadratické funkce Vypočítat a graf.
Y=x²+4x-2 Kvadratické funkce Vypočítat a graf. - Rovnice
 Rovnice -2x²+bx -100 =0 má jeden kořen x1 = 12. Určitě koeficient b a druhý kořen x2.
Rovnice -2x²+bx -100 =0 má jeden kořen x1 = 12. Určitě koeficient b a druhý kořen x2. - Diskriminant
 Určitě diskriminant rovnice: x²+6x+34=1
Určitě diskriminant rovnice: x²+6x+34=1
- Čísla C+D
 Jsou dána čísla C=281, D=201. Určete nejvyšší přirozené číslo S tak, aby podíly C:S, D:S byly se zbytkem 1,
Jsou dána čísla C=281, D=201. Určete nejvyšší přirozené číslo S tak, aby podíly C:S, D:S byly se zbytkem 1, - Zadání 2
 Zadání napište ve zlomku. Doplňte do rámečku číslo tak, aby platila rovnost: (Výsledek zapište zlomkem v základním tvaru. ) 3 · ___ + 1/4 = 5/8
Zadání napište ve zlomku. Doplňte do rámečku číslo tak, aby platila rovnost: (Výsledek zapište zlomkem v základním tvaru. ) 3 · ___ + 1/4 = 5/8 - 3x^2+bx+c=0 82539
 V rovnici 3x²+bx+c=0 je jeden kořen x1 = -3/2. Určete číslo c tak, aby číslo 4 bylo kořenem rovnice. Nápověda - použijte Vietovy vzorce.
V rovnici 3x²+bx+c=0 je jeden kořen x1 = -3/2. Určete číslo c tak, aby číslo 4 bylo kořenem rovnice. Nápověda - použijte Vietovy vzorce. - Prosím 4
 Prosím za x dosaď taková číšla aby naznačené početní úkony byly správné/první a poslední x musí být shodné, děkuji. Příklad: x:2=x -2 y:5=y+7 z*4=z+6
Prosím za x dosaď taková číšla aby naznačené početní úkony byly správné/první a poslední x musí být shodné, děkuji. Příklad: x:2=x -2 y:5=y+7 z*4=z+6 - Platilo 80662
 Je dána funkce y = x² - 4x + 3 Určete všechna reálná čísla z tak, aby platilo g(x) = g(-2).
Je dána funkce y = x² - 4x + 3 Určete všechna reálná čísla z tak, aby platilo g(x) = g(-2).
