Úloha o pohybu
Z křižovatky dvou kolmých silnic vyjeli současně dva cyklisté (každý jinou silnicí) jeden jede průměrnou rychlostí 23 km/h, druhý průměrnou rychlostí 16 km/h. Určete jejich vzájemnou vzdálenost po 30 minutách jízdy.
Správná odpověď:

Zobrazuji 2 komentáře:
Žák
Z křižovatky dvou ulic, které jsou na sebe kolmé, vyjeli dva cyklisté (každý jinou ulicí). Jeden jel rychlostí 18km/h a druhý 24km/h. Jak jsou od sebe vzdáleni po a) 6 minutách, b) 15 minutách?
5 let 1 Like
Tipy na související online kalkulačky
Chcete proměnit jednotku délky?
Chcete proměnit jednotku rychlosti?
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Chcete proměnit jednotky času, např. hodiny na minuty?
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Chcete proměnit jednotku rychlosti?
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Chcete proměnit jednotky času, např. hodiny na minuty?
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
- aritmetika
- odmocnina
- násobení
- dělení
- druhá mocnina
- planimetrie
- Pythagorova věta
- pravoúhlý trojúhelník
- trojúhelník
- čísla
- reálná čísla
Jednotky fyzikálních veličin:
Téma:
Úroveň náročnosti úkolu:
Související a podobné příklady:
- Úhlopříčkou 3
 Úhlopříčkou řezu DBFH pravidelného čtyřbokého hranolu ABCDEFGH je vepsán kruh o průměru 8 cm. Jaký je objem hranolu.
Úhlopříčkou řezu DBFH pravidelného čtyřbokého hranolu ABCDEFGH je vepsán kruh o průměru 8 cm. Jaký je objem hranolu. - Trojúhelníku 83261
 Vypočítejte obsah trojúhelníku ABC, ve kterém znáte stranu c=5 cm, úhel při vrcholu A= 70 stupňů a poměr úseků, které vytíná výška na stranu c je 1:3
Vypočítejte obsah trojúhelníku ABC, ve kterém znáte stranu c=5 cm, úhel při vrcholu A= 70 stupňů a poměr úseků, které vytíná výška na stranu c je 1:3 - Rovnoramenném 83247
 Vypočítejte délky stran v rovnoramenném trojúhelníku, je-li dána výška (na základnu) Vc= 8,8cm a úhel u základny alfa= 38°40`.
Vypočítejte délky stran v rovnoramenném trojúhelníku, je-li dána výška (na základnu) Vc= 8,8cm a úhel u základny alfa= 38°40`. - Obrazec
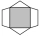 Obrazec se skládá z tmavého čtverce, dvou shodných bílých rovnoramenných trojúhelníků a dvou shodných bílých lichoběžníků. (S každou stranou čtverce splývá základna jednoho bílého útvaru. ) Tmavý čtverec má stranu délky 12 cm a jeho obsah je polovinou obs
Obrazec se skládá z tmavého čtverce, dvou shodných bílých rovnoramenných trojúhelníků a dvou shodných bílých lichoběžníků. (S každou stranou čtverce splývá základna jednoho bílého útvaru. ) Tmavý čtverec má stranu délky 12 cm a jeho obsah je polovinou obs - Zatáčka 3
 Zatáčka má poloměr r = 100 m a je sklopena pod úhlem 20° vůči vodorovné rovině (= úhel klopení). Jaká je bezpečná (ta "nejlepší")rychlost při průjezdu touto zatáčkou? Načrtni obrázek z hlediska NIVS, vyznač síly a vypočítej.
Zatáčka má poloměr r = 100 m a je sklopena pod úhlem 20° vůči vodorovné rovině (= úhel klopení). Jaká je bezpečná (ta "nejlepší")rychlost při průjezdu touto zatáčkou? Načrtni obrázek z hlediska NIVS, vyznač síly a vypočítej. - Vzducholoď
 Vzducholoď je ve výšce x nad zemí. Pavel ji sleduje z místa A pod výškovým úhlem 18 stupnu 26 minut. V tutéž chvíli ji vidí Petr z malého letadla, které zrovna prolétá nad Pavlem ve výšce 150m. Petr vidí vzducholoď pod výškovým úhlem 11 stupnu a 46 minut.
Vzducholoď je ve výšce x nad zemí. Pavel ji sleduje z místa A pod výškovým úhlem 18 stupnu 26 minut. V tutéž chvíli ji vidí Petr z malého letadla, které zrovna prolétá nad Pavlem ve výšce 150m. Petr vidí vzducholoď pod výškovým úhlem 11 stupnu a 46 minut. - Z rozhledně
 Z rozhledně vysoké 40 m je vidět vrchol topolu pod hloubkovym uhlem o velikosti 50*10´a patu topolu v hloubkovem úhlu o velikosti 58*. Vypocitejte výšku topolu.
Z rozhledně vysoké 40 m je vidět vrchol topolu pod hloubkovym uhlem o velikosti 50*10´a patu topolu v hloubkovem úhlu o velikosti 58*. Vypocitejte výšku topolu. - Dopravní 2
 Dopravní letadlo, které právě prolétá nad místem 2 400 m vzdáleném od místa pozorovatele, je vidět pod výškovým úhlem o velikosti 26° 20´. V jaké výšce letadlo letí?
Dopravní letadlo, které právě prolétá nad místem 2 400 m vzdáleném od místa pozorovatele, je vidět pod výškovým úhlem o velikosti 26° 20´. V jaké výšce letadlo letí? - Pravoúhlý 37
 Pravoúhlý trojúhelník má obsah 36 cm². V něm je umístěn čtverec tak, že dvě strany čtverce jsou částmi dvou stran trojúhelníku a jeden vrchol čtverce je ve třetině nejdelší strany. Určete obsah tohoto čtverce.
Pravoúhlý trojúhelník má obsah 36 cm². V něm je umístěn čtverec tak, že dvě strany čtverce jsou částmi dvou stran trojúhelníku a jeden vrchol čtverce je ve třetině nejdelší strany. Určete obsah tohoto čtverce. - Pozemek 19
 Pozemek na stavbu rodinných domů má tvar pravoúhleho lichoběžníka se základnami délek 21m a 11,2m. Při ceně 2500 Kč za metr čtvereční je hodnota pozemku vyčíslena na 1352400 Kc. Jaká by byla délka pletiva potřebného k oplocení tohoto pozemku?
Pozemek na stavbu rodinných domů má tvar pravoúhleho lichoběžníka se základnami délek 21m a 11,2m. Při ceně 2500 Kč za metr čtvereční je hodnota pozemku vyčíslena na 1352400 Kc. Jaká by byla délka pletiva potřebného k oplocení tohoto pozemku? - Je dán 26
 Je dán rotační kužel s poloměrem 32 cm a délkou boční strany s = 65 cm. Vypočtěte povrch a objem
Je dán rotační kužel s poloměrem 32 cm a délkou boční strany s = 65 cm. Vypočtěte povrch a objem - Vypočítejte 82693
 Vypočítejte výšku stožáru, jehož patu vidíme v hloubkovém úhlu 11° a vrchol ve výškovém úhlu 28°. Stožár je pozorován z místa 10 m nad úrovní paty stožáru.
Vypočítejte výšku stožáru, jehož patu vidíme v hloubkovém úhlu 11° a vrchol ve výškovém úhlu 28°. Stožár je pozorován z místa 10 m nad úrovní paty stožáru. - Je dán 25
 Je dán rotační kužel s výškou 18 cm a délkou boční strany s = 45 cm. Vypočtěte povrch a objem
Je dán rotační kužel s výškou 18 cm a délkou boční strany s = 45 cm. Vypočtěte povrch a objem - Napište 3
 Napište rovnici kružnice, která prochází body Q[3,5], R[2,6] a má střed na přímce 2x+3y-4=0.
Napište rovnici kružnice, která prochází body Q[3,5], R[2,6] a má střed na přímce 2x+3y-4=0. - Rovnoběžníku 82626
 Vypočítejte obsah rovnoběžníku, pokud známe obvod je 23 cm, úhlopříčka je 8,5 cm a jedna strana je o 1,5 cm delší.
Vypočítejte obsah rovnoběžníku, pokud známe obvod je 23 cm, úhlopříčka je 8,5 cm a jedna strana je o 1,5 cm delší. - Žebřík 16
 Žebřík má délku 7 metrů a je opřen o zeď tak, že jeho dolní konec zdu je vzdálen 4 metry, Urči do jaké výšky dosahuje žebřík
Žebřík má délku 7 metrů a je opřen o zeď tak, že jeho dolní konec zdu je vzdálen 4 metry, Urči do jaké výšky dosahuje žebřík - Jeřáb 3
 Jeřáb zvedá náklad rovnoměrným přímočarým pohybem do výšky 8 m a současně se posunuje vodorovným směrem do vzdálenosti 6 m. Jakou dráhu přitom náklad urazil? Jak velkou výslednou rychlostí se náklad pohyboval, trvalo-li jeho přemistění 50 s
Jeřáb zvedá náklad rovnoměrným přímočarým pohybem do výšky 8 m a současně se posunuje vodorovným směrem do vzdálenosti 6 m. Jakou dráhu přitom náklad urazil? Jak velkou výslednou rychlostí se náklad pohyboval, trvalo-li jeho přemistění 50 s
