Lichoběžník MO
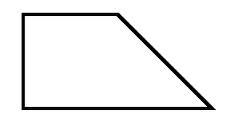
Je dán pravouhlý lichoběžník ABCD s pravým uhlem u bodu B, |AC| = 12, |CD| = 8, uhlopříčky jsou na sebe kolmé.
Vypočítejte obvod a obsah takéhoto lichobežníka.
Vypočítejte obvod a obsah takéhoto lichobežníka.
Správná odpověď:
Zobrazuji 3 komentáře:
Žák
mám za to, že cos(x)2+sin(x)2=1. Vy ale počítáte s tím, že 2cos(x)2=1. A to je asi blb2, ne?
4 roky 1 Like
Žák
Za předpokladu, že jsou zadány délky uhlopříček |AC| = 12 cm a |BD| = 8 cm je plocha příslušného pravoúhlého lichoběžníka 54 cm2 a obvod cca 30,5 cm.
Dr Math
Zadani neni jednoznacne, protoze dva vrcholy lichobeznika jsou s pravym uhlem, a tim neni jiste, ktery vrchol je bod B. Rovnez neni jasne orientace oznaceni vrcholu lichobeznika. Reseni prikladu by usnadnilo, kdyby v obrazku byly popsany vrcholy lichobeznika - A, B, C, D.
Tipy na související online kalkulačky
Hledáte pomoc s výpočtem kořenů kvadratické rovnice?
Potřebujete pomoci sčítat, zkrátít či vynásobit zlomky? Zkuste naši zlomkovou kalkulačku.
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte si převody jednotek úhlů úhlové stupně, minuty, sekundy, radiány.
Potřebujete pomoci sčítat, zkrátít či vynásobit zlomky? Zkuste naši zlomkovou kalkulačku.
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte si převody jednotek úhlů úhlové stupně, minuty, sekundy, radiány.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
- algebra
- kvadratická rovnice
- rovnice
- aritmetika
- odmocnina
- planimetrie
- Pythagorova věta
- pravoúhlý trojúhelník
- obsah
- obvod
- trojúhelník
- lichoběžník
- úhlopříčka
- základní funkce
- úvaha
- čísla
- zlomky
- goniometrie a trigonometrie
- sinus
- kosinus
- tangens
- arkustangens
- arkussinus
- arkuskosinus
Jednotky fyzikálních veličin:
Úroveň náročnosti úkolu:
Související a podobné příklady:
- Těžítko 3
 Těžítko ze skla má tvar pravidelného čtyřbokého jehlanu o hraně podstavy 10cm. Stěny pláště jsou rovnostranné trojúhelníky. Jakou hmotnost v gramech má těžítko, jestliže hustota skla je 2500kg/m³?
Těžítko ze skla má tvar pravidelného čtyřbokého jehlanu o hraně podstavy 10cm. Stěny pláště jsou rovnostranné trojúhelníky. Jakou hmotnost v gramech má těžítko, jestliže hustota skla je 2500kg/m³? - Trojúhelníku 83261
 Vypočítejte obsah trojúhelníku ABC, ve kterém znáte stranu c=5 cm, úhel při vrcholu A= 70 stupňů a poměr úseků, které vytíná výška na stranu c je 1:3
Vypočítejte obsah trojúhelníku ABC, ve kterém znáte stranu c=5 cm, úhel při vrcholu A= 70 stupňů a poměr úseků, které vytíná výška na stranu c je 1:3 - Vypočítej 83251
 Vypočítej obvod čtverce, jehož obsah je 25 dm² .
Vypočítej obvod čtverce, jehož obsah je 25 dm² . - Krychle 50
 Krychle ABCDEFGH má hranu délky 3 cm. Vypočítejte objem jehlanu ABCDH.
Krychle ABCDEFGH má hranu délky 3 cm. Vypočítejte objem jehlanu ABCDH. - Osový řez válce
 Osovým řezem válce je čtverec o obsahu 56,25 cm². Vypočítejte jeho povrch a objem. Výsledek vyjádřete ve čtverečných decimetrech a v krychlových decimetrech a zaokrouhlete na setiny.
Osovým řezem válce je čtverec o obsahu 56,25 cm². Vypočítejte jeho povrch a objem. Výsledek vyjádřete ve čtverečných decimetrech a v krychlových decimetrech a zaokrouhlete na setiny. - Pilíř 3
 Kolik betonu je třeba na vylití 8 betonových sloupů s podstavou čtverce: a = 38cm, výška sloupů je 6,2m? V každém sloupu je dutina válce o průměru 15cm.
Kolik betonu je třeba na vylití 8 betonových sloupů s podstavou čtverce: a = 38cm, výška sloupů je 6,2m? V každém sloupu je dutina válce o průměru 15cm. - Obdélníku 83176
 Pokud zmenšíme délku obdélníku o 2cm a šířku o 1cm, tak se obsah obdélníku zmenší o 8 cm². Pokud zvětšíme délku obdélníku o 1cm a šířku o 2cm, tak se obsah obdélníku zvětší o 13 cm². Jaké byly původní rozměry obdélníku?
Pokud zmenšíme délku obdélníku o 2cm a šířku o 1cm, tak se obsah obdélníku zmenší o 8 cm². Pokud zvětšíme délku obdélníku o 1cm a šířku o 2cm, tak se obsah obdélníku zvětší o 13 cm². Jaké byly původní rozměry obdélníku? - Obrazec
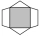 Obrazec se skládá z tmavého čtverce, dvou shodných bílých rovnoramenných trojúhelníků a dvou shodných bílých lichoběžníků. (S každou stranou čtverce splývá základna jednoho bílého útvaru. ) Tmavý čtverec má stranu délky 12 cm a jeho obsah je polovinou obs
Obrazec se skládá z tmavého čtverce, dvou shodných bílých rovnoramenných trojúhelníků a dvou shodných bílých lichoběžníků. (S každou stranou čtverce splývá základna jednoho bílého útvaru. ) Tmavý čtverec má stranu délky 12 cm a jeho obsah je polovinou obs - Farmár 7
 Farmár má ustájených 250 kráv. V kravíne pripadá na jednu kravu 5m². O koľko m² sa zmenší miesto pre jednu kravu, keď ich počet stúpne o 26?
Farmár má ustájených 250 kráv. V kravíne pripadá na jednu kravu 5m². O koľko m² sa zmenší miesto pre jednu kravu, keď ich počet stúpne o 26? - V kanceláři 2
 V kanceláři máme vyčleněny prostor pro skříň o šířce 60cm. Můžeme koupit skříň o výšce 180cm a ploše přední stěny 126dm²?
V kanceláři máme vyčleněny prostor pro skříň o šířce 60cm. Můžeme koupit skříň o výšce 180cm a ploše přední stěny 126dm²? - Katka 7
 Katka si objednala dort ve tvaru valce o objemu 15,7l. Skládá se ze dvou pater. Objem horního patra je 4x menší než objem dolního patra. Výška obou pater stejna a je rovná polomeru horního patra dortu. Katka rozkrojila dort kolmo k podložce na 2 stejně čá
Katka si objednala dort ve tvaru valce o objemu 15,7l. Skládá se ze dvou pater. Objem horního patra je 4x menší než objem dolního patra. Výška obou pater stejna a je rovná polomeru horního patra dortu. Katka rozkrojila dort kolmo k podložce na 2 stejně čá - Plášť válce 3
 Obsah pláště rotačního válce je třikrát větší než obsah jedné podstavy tohoto válce. Poloměr podstavy válce je 10 cm. Jaký je povrch válce?
Obsah pláště rotačního válce je třikrát větší než obsah jedné podstavy tohoto válce. Poloměr podstavy válce je 10 cm. Jaký je povrch válce? - Prosím 6
 Prosím o vyjádření r ze vzorce pro povrch válce.
Prosím o vyjádření r ze vzorce pro povrch válce. - Krabice
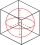 Kolik dm² tapety je třeba na polepení krabice (bez víka) tvaru krychle o hraně 12 dm?
Kolik dm² tapety je třeba na polepení krabice (bez víka) tvaru krychle o hraně 12 dm? - Jaké množství
 Jaké množství betonu je třeba objednat pro vybetonování rodinného domu obdélníkového půdorysu o rozměrech 15 m × 12,6 m při použití ztraceného bednění. Hloubka základů tvořený ztracenými bedněním je stanovena na 80cm. Použitý beton tvoří 80% objemu tvárni
Jaké množství betonu je třeba objednat pro vybetonování rodinného domu obdélníkového půdorysu o rozměrech 15 m × 12,6 m při použití ztraceného bednění. Hloubka základů tvořený ztracenými bedněním je stanovena na 80cm. Použitý beton tvoří 80% objemu tvárni - Poměr 51
 Poměr vzdálenosti nejbližšího a nejvzdálenějšího bodu kružnice, která je popsána rovnicí x2+y2-16x-12y+75=0 od počátku soustavy souřadnic je?
Poměr vzdálenosti nejbližšího a nejvzdálenějšího bodu kružnice, která je popsána rovnicí x2+y2-16x-12y+75=0 od počátku soustavy souřadnic je? - Pravoúhlý 37
 Pravoúhlý trojúhelník má obsah 36 cm². V něm je umístěn čtverec tak, že dvě strany čtverce jsou částmi dvou stran trojúhelníku a jeden vrchol čtverce je ve třetině nejdelší strany. Určete obsah tohoto čtverce.
Pravoúhlý trojúhelník má obsah 36 cm². V něm je umístěn čtverec tak, že dvě strany čtverce jsou částmi dvou stran trojúhelníku a jeden vrchol čtverce je ve třetině nejdelší strany. Určete obsah tohoto čtverce.
