Zkratka
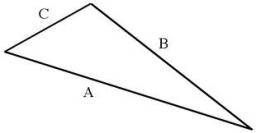
Představte si, že jdete ke kamarádovi po rovné cestě. Ta cesta má délku 350 metrů. Potom zahnete doprava a půjdete dalších 1790 metrů a jste u kamaráda.
Otázka zní, o kolik bude kratší cesta, když půjdete přímou cestou přes pole?
Otázka zní, o kolik bude kratší cesta, když půjdete přímou cestou přes pole?
Správná odpověď:
Zobrazuji 2 komentáře:
Žák
Tato slovní úloha byla v Pythagoriadě a opravdu mi nepříjde ,že žáci 7 třídy by toto vypičítaly.Rovnice, Pythagorovu větu,odmocniny a planimetrii se ještě neučili !!!!
Tipy na související online kalkulačky
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Chcete proměnit jednotku délky?
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Chcete proměnit jednotku délky?
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
- algebra
- rovnice
- aritmetika
- odmocnina
- druhá mocnina
- sčítání
- odčítání
- planimetrie
- Pythagorova věta
- pravoúhlý trojúhelník
- obvod
- trojúhelník
- čísla
- reálná čísla
Jednotky fyzikálních veličin:
Téma:
Úroveň náročnosti úkolu:
Související a podobné příklady:
- 3x^2+bx+c=0 82539
 V rovnici 3x²+bx+c=0 je jeden kořen x1 = -3/2. Určete číslo c tak, aby číslo 4 bylo kořenem rovnice. Nápověda - použijte Vietovy vzorce.
V rovnici 3x²+bx+c=0 je jeden kořen x1 = -3/2. Určete číslo c tak, aby číslo 4 bylo kořenem rovnice. Nápověda - použijte Vietovy vzorce. - Poloha 2
 Poloha hmotného bodu, který se pohybuje podél osy x, je dána vztahem x=10t²-5t. Vyjádřete jeho rychlost a zrychlení.
Poloha hmotného bodu, který se pohybuje podél osy x, je dána vztahem x=10t²-5t. Vyjádřete jeho rychlost a zrychlení. - Dokonalý čtverec
 Klasifikovali byste 324 jako dokonalý čtverec, dokonalou kostku, obojí nebo ani jedno? ...
Klasifikovali byste 324 jako dokonalý čtverec, dokonalou kostku, obojí nebo ani jedno? ... - Klasifikujte: 80835
 Vypočítejte BMI a poté klasifikujte: 1 hmotnost - 35 kg Výška - 1,25 m 2 hmotnost - 40 kg Výška - 1,40 m 3 hmotnost - 50 kg Výška-1,75 m 4 hmotnost-55 kg Výška-1,65 m 5 hmotnost-63 kg Výška-1,23 m
Vypočítejte BMI a poté klasifikujte: 1 hmotnost - 35 kg Výška - 1,25 m 2 hmotnost - 40 kg Výška - 1,40 m 3 hmotnost - 50 kg Výška-1,75 m 4 hmotnost-55 kg Výška-1,65 m 5 hmotnost-63 kg Výška-1,23 m - V=4x^3+43x^2+63x 72764
 Největší vnitřní akvárium na světě. Ve své obrovské nádrži s kapacitou reprezentovanou následujícím polynomem V=4x³+43x²+63x Akvárium má tvar obdélníkového hranolu. Najděte následující: 1. Je-li výška akvária x, najděte plochu základny (B). 2. Na základě
Největší vnitřní akvárium na světě. Ve své obrovské nádrži s kapacitou reprezentovanou následujícím polynomem V=4x³+43x²+63x Akvárium má tvar obdélníkového hranolu. Najděte následující: 1. Je-li výška akvária x, najděte plochu základny (B). 2. Na základě - Kolikrát 27
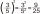 Kolikrát větší je rozdíl druhých mocnin čísel 4 a 2 než druhá mocnina jejich rozdílu (v uvedeném pořadí)?
Kolikrát větší je rozdíl druhých mocnin čísel 4 a 2 než druhá mocnina jejich rozdílu (v uvedeném pořadí)? - Kolikrát 26
 Vypočtěte, kolikrát je druhá mocnina čísla 1/100 menší než 1/1000. (čísla uvedené ve zlomku)
Vypočtěte, kolikrát je druhá mocnina čísla 1/100 menší než 1/1000. (čísla uvedené ve zlomku) - Hodnota
 Když x = 3 a y = 5, o kolik hodnota 3x² – 2y převyšuje hodnotu 2x² – 3y?
Když x = 3 a y = 5, o kolik hodnota 3x² – 2y převyšuje hodnotu 2x² – 3y? - Přirozené 55591
 Pokud n je přirozené číslo, které dává při dělení 5 zbytek 2 nebo 3, tak n na druhou dává při dělení 5 zbytek 4. Dokažte přímo
Pokud n je přirozené číslo, které dává při dělení 5 zbytek 2 nebo 3, tak n na druhou dává při dělení 5 zbytek 4. Dokažte přímo - Neznámými: 50403
 Dělení zlomků s neznámými: Zlomek 1: Množství x na druhou plus 6 krát x plus 9 nad množství x minus 1. Zlomek 2: množství x na druhou minus 9 oproti množství x na druhou minus 2 krát x plus 1. Najděte zlomek 1 nad zlomkem 2.
Dělení zlomků s neznámými: Zlomek 1: Množství x na druhou plus 6 krát x plus 9 nad množství x minus 1. Zlomek 2: množství x na druhou minus 9 oproti množství x na druhou minus 2 krát x plus 1. Najděte zlomek 1 nad zlomkem 2. - Spotřeboval 48761
 Matouš maluje svůj pokoj. Maluje stěny tvaru čtverce. Když vymaloval stěnu se stranou 3 m, spotřeboval 5kg barvy. Kolik kg barvy bude potřebovat na zeď o straně délky 6 m?
Matouš maluje svůj pokoj. Maluje stěny tvaru čtverce. Když vymaloval stěnu se stranou 3 m, spotřeboval 5kg barvy. Kolik kg barvy bude potřebovat na zeď o straně délky 6 m? - Pan Duma
 Pan Duma nedávno zdědil obdélníkový pozemek, část majetku, který zanechal jeho zesnulý otec. Pozemek o následujících rozměrech: Délka=2x+1;Šířka=x-1. Určete vzorec pomocí proměnné x, který nejlépe popisuje plochu obdélníkového pozemku. Na pozemku má v plá
Pan Duma nedávno zdědil obdélníkový pozemek, část majetku, který zanechal jeho zesnulý otec. Pozemek o následujících rozměrech: Délka=2x+1;Šířka=x-1. Určete vzorec pomocí proměnné x, který nejlépe popisuje plochu obdélníkového pozemku. Na pozemku má v plá - Vypočítejte 48
 Vypočítejte obsah kruhu, který má obvod 314 cm.
Vypočítejte obsah kruhu, který má obvod 314 cm. - 30metrový 45481
 30metrový strom se zlomil. Jeho vrcholec spadl 5m od kmene. V jaké výši se zlomil?
30metrový strom se zlomil. Jeho vrcholec spadl 5m od kmene. V jaké výši se zlomil? - Květinová
 Květinová zahrada má tvar čtverce. Nová zahrada má tvar obdélníku a její jeden rozměr je o 8 m menší a druhý je dvojnásobně větší než ve čtvercové zahradě. Jaké rozměry měla původní zahrada i nová zahrada, jestliže výměra obou zahrad je stejná?
Květinová zahrada má tvar čtverce. Nová zahrada má tvar obdélníku a její jeden rozměr je o 8 m menší a druhý je dvojnásobně větší než ve čtvercové zahradě. Jaké rozměry měla původní zahrada i nová zahrada, jestliže výměra obou zahrad je stejná? - Poseidon
 Poseidon vložil 2 747 zlatých drachem na spořicí účet univerzity Mount Olympus, aby zajistil, že Percy může jít na vysokou školu. Platí roční úroky 0,04 (v desetinné podobě). Po 11 letech vybere peníze. O kolik více peněz by měl, kdyby se úrok vyplácel sp
Poseidon vložil 2 747 zlatých drachem na spořicí účet univerzity Mount Olympus, aby zajistil, že Percy může jít na vysokou školu. Platí roční úroky 0,04 (v desetinné podobě). Po 11 letech vybere peníze. O kolik více peněz by měl, kdyby se úrok vyplácel sp - Vyjádřeny 40401
 Vypočítej průměr kruhu jehož obsah v cm² a obvod v cm jsou vyjádřeny stejným číslem.
Vypočítej průměr kruhu jehož obsah v cm² a obvod v cm jsou vyjádřeny stejným číslem.
