Čtyřboký jehlan
Pravidelný čtyřboký jehlan má délku podstavné hrany 6 cm a délka boční hrany je 9 centimetrů. Vypočítejte objem a obsah
Správná odpověď:
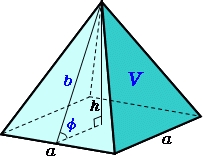
Tipy na související online kalkulačky
Chcete proměnit jednotku délky?
Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu.
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu.
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
- algebra
- vyjádření neznámé ze vzorce
- stereometrie
- jehlan
- povrch tělesa
- planimetrie
- Pythagorova věta
- pravoúhlý trojúhelník
- trojúhelník
- čtyřúhelník
Jednotky fyzikálních veličin:
Úroveň náročnosti úkolu:
Související a podobné příklady:
- Spádnice
 Určit objem a povrch kužele, jehož spádnice o délce 8cm svírá s rovinou podstavy úhel 75 stupňů
Určit objem a povrch kužele, jehož spádnice o délce 8cm svírá s rovinou podstavy úhel 75 stupňů - Objem 31
 Objem kvádru je 7 500 dm³. Délky hran jsou v poměru 3 : 4 : 5. Vypočtěte povrch kvádru.
Objem kvádru je 7 500 dm³. Délky hran jsou v poměru 3 : 4 : 5. Vypočtěte povrch kvádru. - Objem 30
 Objem kvádru je 960 cm³. Délky hran jsou v poměru 1 : 3 : 5. Vypočtěte povrch kvádru.
Objem kvádru je 960 cm³. Délky hran jsou v poměru 1 : 3 : 5. Vypočtěte povrch kvádru. - Vypočítejte 70294
 Délky hran čtyřbokého hranolu jsou v poměru a: b:c = 2:4:5. Povrch hranolu je 57 cm². Vypočítejte objem.
Délky hran čtyřbokého hranolu jsou v poměru a: b:c = 2:4:5. Povrch hranolu je 57 cm². Vypočítejte objem.
- Krabice na mléko
 Monika si změřila rozměry dvou různých krabic na mléko. Jedna měla rozměry 9*5,8*19,6 cm, druhá 9,4*6,3*17,3 cm. Zaujalo ji, zda se na výrobu některé krabice spotřebuje méně materiálu. Ověř to a zjisti, kolik procent materiálu se ušetří. (Materiál na zalo
Monika si změřila rozměry dvou různých krabic na mléko. Jedna měla rozměry 9*5,8*19,6 cm, druhá 9,4*6,3*17,3 cm. Zaujalo ji, zda se na výrobu některé krabice spotřebuje méně materiálu. Ověř to a zjisti, kolik procent materiálu se ušetří. (Materiál na zalo - Vypočítejte 62864
 Objem kvádru je 1440 cm3, jeho povrch je 792 cm² a obsah jedné jeho stěny je 92 cm². Vypočítejte délky jeho stran.
Objem kvádru je 1440 cm3, jeho povrch je 792 cm² a obsah jedné jeho stěny je 92 cm². Vypočítejte délky jeho stran. - Spotřebovali 62064
 Otevřená krabička má tvar kostky. Na její oblepení spotřebovali 80 dm² papíru. Jaký je objem této krabičky?
Otevřená krabička má tvar kostky. Na její oblepení spotřebovali 80 dm² papíru. Jaký je objem této krabičky? - Vypočítejte 61944
 Vypočítejte objem a povrch planety Venuše, pokud její obvod je 12 000km.
Vypočítejte objem a povrch planety Venuše, pokud její obvod je 12 000km. - Hranol RRPT
 Vypočítejte objem a povrch hranolu o výšce 120mm, jehož podstavce je rovnoramenný trojúhelník s odvěsnou dlouhou 5cm.
Vypočítejte objem a povrch hranolu o výšce 120mm, jehož podstavce je rovnoramenný trojúhelník s odvěsnou dlouhou 5cm.
- Roviny bočních stěn
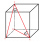 Vypočítej objem a povrch kvádru jehož strana c má délku 30 cm a tělesová úhlopříčka svírá s rovinami bočních stěn úhly o velikostech 24 st. 20’, 45 st. 30’
Vypočítej objem a povrch kvádru jehož strana c má délku 30 cm a tělesová úhlopříčka svírá s rovinami bočních stěn úhly o velikostech 24 st. 20’, 45 st. 30’ - Seříznutého 58663
 Ocelovou součástku ve tvaru seříznutého čtyřbokého jehlanu roztavili a vyrobili tři identické kostky. Určete povrch jedné kostky, pokud hrany postav jehlanu jsou 30 mm a 80 mm a výška jehlanu je 60 mm. Nevím si s tím nijak rády, nenašel jsem nikde řešení
Ocelovou součástku ve tvaru seříznutého čtyřbokého jehlanu roztavili a vyrobili tři identické kostky. Určete povrch jedné kostky, pokud hrany postav jehlanu jsou 30 mm a 80 mm a výška jehlanu je 60 mm. Nevím si s tím nijak rády, nenašel jsem nikde řešení - 3S hranol
 Najděte objem a povrch trojúhelníkového hranolu s pravoúhlým trojúhelníkovým dnem, pokud je délka odvěsen dna hranolu je 7,2 cm a 4,7 cm a výška hranolu je 24 cm.
Najděte objem a povrch trojúhelníkového hranolu s pravoúhlým trojúhelníkovým dnem, pokud je délka odvěsen dna hranolu je 7,2 cm a 4,7 cm a výška hranolu je 24 cm. - Pravidelný 11
 Pravidelný trojboký jehlan ABCDV má délku podstavné hrany a=8 cm a výšku 7 cm. Vypočítej povrch a objem jehlanu
Pravidelný trojboký jehlan ABCDV má délku podstavné hrany a=8 cm a výšku 7 cm. Vypočítej povrch a objem jehlanu - Mléko tetrapack
 Krabice tvaru krychle je po okraj naplněna mlékem o objemu 2 litry. Vypočítej hranu a povrch krabice.
Krabice tvaru krychle je po okraj naplněna mlékem o objemu 2 litry. Vypočítej hranu a povrch krabice.
- Krychle 50
 Krychle ABCDEFGH má hranu délky 3 cm. Vypočítejte objem jehlanu ABCDH.
Krychle ABCDEFGH má hranu délky 3 cm. Vypočítejte objem jehlanu ABCDH. - Osový řez válce
 Osovým řezem válce je čtverec o obsahu 56,25 cm². Vypočítejte jeho povrch a objem. Výsledek vyjádřete ve čtverečných decimetrech a v krychlových decimetrech a zaokrouhlete na setiny.
Osovým řezem válce je čtverec o obsahu 56,25 cm². Vypočítejte jeho povrch a objem. Výsledek vyjádřete ve čtverečných decimetrech a v krychlových decimetrech a zaokrouhlete na setiny. - Pilíř 3
 Kolik betonu je třeba na vylití 8 betonových sloupů s podstavou čtverce: a = 38cm, výška sloupů je 6,2m? V každém sloupu je dutina válce o průměru 15cm.
Kolik betonu je třeba na vylití 8 betonových sloupů s podstavou čtverce: a = 38cm, výška sloupů je 6,2m? V každém sloupu je dutina válce o průměru 15cm.
