Gon funkce
Rozhodněte, které z čísel (hodnot goniometrických funkcí) jsou kladné a které záporné (nebo nulové). Kladné označte +1 a záporné -1.
Správná odpověď:
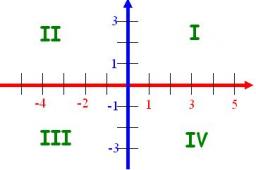
Tipy na související online kalkulačky
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Jednotky fyzikálních veličin:
Úroveň náročnosti úkolu:
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Vektorovou 18193
 Nechť v = (1, 2, 1), u = (0, -1, 3) a w = (1, 0, 7) . Vyřešte vektorovou rovnici c1 v + c2 u + c3 w = 0 pro proměnné c1, c2, c3 a rozhodněte, zda vektory v, u a w jsou lineárně závislé nebo nezávislé
Nechť v = (1, 2, 1), u = (0, -1, 3) a w = (1, 0, 7) . Vyřešte vektorovou rovnici c1 v + c2 u + c3 w = 0 pro proměnné c1, c2, c3 a rozhodněte, zda vektory v, u a w jsou lineárně závislé nebo nezávislé - Nulové body
 Vypočítejte kořeny rovnice: 1 |x +4| -2 |x -9| +4 |x +3| = 42
Vypočítejte kořeny rovnice: 1 |x +4| -2 |x -9| +4 |x +3| = 42 - Z=-√2-√2i 74744
 Nechť komplexní číslo z=-√2-√2i, kde i² = -1. Najděte |z|, arg(z), z* (kde * označuje komplexní konjugát) a (1/z). V případě potřeby napište své odpovědi ve tvaru a + i b, kde ai b jsou reálná čísla. Označte polohy čísel z, z* a (1/z) na Argandově diagram
Nechť komplexní číslo z=-√2-√2i, kde i² = -1. Najděte |z|, arg(z), z* (kde * označuje komplexní konjugát) a (1/z). V případě potřeby napište své odpovědi ve tvaru a + i b, kde ai b jsou reálná čísla. Označte polohy čísel z, z* a (1/z) na Argandově diagram - Kvadr. funcke
 Které z bodů patří funkcí f:y= 2x²- 3x + 1 : A(-2, 15) B (3,10) C (1,4)
Které z bodů patří funkcí f:y= 2x²- 3x + 1 : A(-2, 15) B (3,10) C (1,4) - Rovnice 39
 Rovnice linearní funkcí je : y=-3x+4 a) urči průsečíky s osami načrtni graf b) pro které x platí f(x)=-1 c) pro které x platí f(x)=0 d) pro které y platí f(-1/2)=y
Rovnice linearní funkcí je : y=-3x+4 a) urči průsečíky s osami načrtni graf b) pro které x platí f(x)=-1 c) pro které x platí f(x)=0 d) pro které y platí f(-1/2)=y - Lichoběžníku 44431
 1. V kartézském rámci o funkcích f a g víme, že: funkce (f) je definována vztahem f (x) = 2x², funkce (g) je definována vztahem g (x) = x + 3, bod (O) je počátkem reference, bod (C) je průsečík grafu funkce (g) s osou pořadnice, body A a B jsou průsečíky
1. V kartézském rámci o funkcích f a g víme, že: funkce (f) je definována vztahem f (x) = 2x², funkce (g) je definována vztahem g (x) = x + 3, bod (O) je počátkem reference, bod (C) je průsečík grafu funkce (g) s osou pořadnice, body A a B jsou průsečíky - Leží/neleži
 Funkce je dána předpisem f(x) = 8x+16. Zjistěte, zda bod D[-1; 8] náleží funkci. Úlohu řešte graficky nebo početně a odpověď zdůvodněte.
Funkce je dána předpisem f(x) = 8x+16. Zjistěte, zda bod D[-1; 8] náleží funkci. Úlohu řešte graficky nebo početně a odpověď zdůvodněte. - Potřebujete 83054
 Žádný problém; Zde je pět problémů s desetinném sečtením, které si můžete procvičit: 1. Jaký je výsledek 3,5 + 2,1? 2. Jaký je výsledek 0,8 + 0,3? 3. Jaký je výsledek 5,2 + 1,7? 4. Jaký je výsledek 2,5 + 0,9? 5. Jaký je výsledek 1,4 + 0,6? Doufám, že tyto
Žádný problém; Zde je pět problémů s desetinném sečtením, které si můžete procvičit: 1. Jaký je výsledek 3,5 + 2,1? 2. Jaký je výsledek 0,8 + 0,3? 3. Jaký je výsledek 5,2 + 1,7? 4. Jaký je výsledek 2,5 + 0,9? 5. Jaký je výsledek 1,4 + 0,6? Doufám, že tyto - Vypočítejte 48141
 Vypočítejte a zapište do tabulky 10 hodnot funkce f: y=3x+1 az nich graf funkce
Vypočítejte a zapište do tabulky 10 hodnot funkce f: y=3x+1 az nich graf funkce - Vypočítejte 34921
 Postupně jsme naměřili hodnoty 3,8,13,10,1,13,10,5,3,9. Vypočítejte o kolik je větší součet mediánu a průměru tohoto souboru od modusu tohoto souboru.
Postupně jsme naměřili hodnoty 3,8,13,10,1,13,10,5,3,9. Vypočítejte o kolik je větší součet mediánu a průměru tohoto souboru od modusu tohoto souboru. - Lineárni funkce
 Pokud použijeme jednu z následujících funkcí x + p = q nebo px = q, napište na reprezentaci těchto problémů pomocí x jako neznámé proměnné: Larry běžel o 7 kilometrů více než Barry za měsíc, pokud Larry utíkal 20 kilometrů, kolik Barry uběhl?
Pokud použijeme jednu z následujících funkcí x + p = q nebo px = q, napište na reprezentaci těchto problémů pomocí x jako neznámé proměnné: Larry běžel o 7 kilometrů více než Barry za měsíc, pokud Larry utíkal 20 kilometrů, kolik Barry uběhl? - Atléti
 Všichni chlapci atletického oddílu se seřadili do zastupu podle velikosti. Před Petrem stála jedna osmina celkového počtu. Hned za Petrem stál jeho bratr Radek a za Radkem ještě pět šestin celkového počtu chlapců. Neznámý celkový počet chlapců atletického
Všichni chlapci atletického oddílu se seřadili do zastupu podle velikosti. Před Petrem stála jedna osmina celkového počtu. Hned za Petrem stál jeho bratr Radek a za Radkem ještě pět šestin celkového počtu chlapců. Neznámý celkový počet chlapců atletického - Číselna os 2
 Na přímce představující číselnou osu uvažte navzájem různé body odpovídající číslům a, 2a, 3a+1 ve všech možných pořadích. U každé možnosti rozhodněte, zda je takové uspořádání možné. Pokud ano, uveďte konkrétní příklad, pokud ne, zdůvodněte proč.
Na přímce představující číselnou osu uvažte navzájem různé body odpovídající číslům a, 2a, 3a+1 ve všech možných pořadích. U každé možnosti rozhodněte, zda je takové uspořádání možné. Pokud ano, uveďte konkrétní příklad, pokud ne, zdůvodněte proč. - Protíná úsečku
 Rozhodněte, zda přímka p: x + 2 y - 7 = 0 protíná úsečku danou body A [1, 1] a B [5, 3]
Rozhodněte, zda přímka p: x + 2 y - 7 = 0 protíná úsečku danou body A [1, 1] a B [5, 3] - Mirek a Zuzka
 Obdélník je rozdělený na 7 políček. Na každé políčko se má napsat právě jedno z čísel 1, 2 a 3. Mirek tvrdí, že to lze provést tak, aby součet dvou vedle sebe napsaných čísel byl pokaždé jiný. Zuzka naopak tvrdí, že to možné není. Rozhodněte, kdo z nich m
Obdélník je rozdělený na 7 políček. Na každé políčko se má napsat právě jedno z čísel 1, 2 a 3. Mirek tvrdí, že to lze provést tak, aby součet dvou vedle sebe napsaných čísel byl pokaždé jiný. Zuzka naopak tvrdí, že to možné není. Rozhodněte, kdo z nich m - Pravoúhlý 33
 Pravoúhlý trojúhelník KLM s pravým úhlem při vrcholu L, uhlem beta při vrcholu K a uhlem alfa u vrcholu M. Úhel u vrcholu M = 65°, strana l = 17,5 cm. Pomoci Pythagorovy věty a goniometrických funkci vypočítáte délky všech stran a úhel při vrcholu K.
Pravoúhlý trojúhelník KLM s pravým úhlem při vrcholu L, uhlem beta při vrcholu K a uhlem alfa u vrcholu M. Úhel u vrcholu M = 65°, strana l = 17,5 cm. Pomoci Pythagorovy věty a goniometrických funkci vypočítáte délky všech stran a úhel při vrcholu K. - Zjistil 81699
 Na hřišti se hraje přesně 1/6 dětí. Přesně 3/5 dětí hraje fotbal. Jack přidá 1/6 + 3/5, aby zjistil celkový zlomek dětí v parku, které si hrají na hřišti nebo hrají fotbal. Má pravdu?
Na hřišti se hraje přesně 1/6 dětí. Přesně 3/5 dětí hraje fotbal. Jack přidá 1/6 + 3/5, aby zjistil celkový zlomek dětí v parku, které si hrají na hřišti nebo hrají fotbal. Má pravdu?
