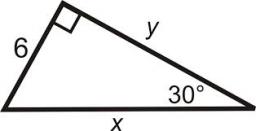
30-60-90
The longer leg of a 30°-60°-90° triangle measures 5. What is the length of the shorter leg?
Correct answer:
Tips for related online calculators
Do you want to convert length units?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Calculate 47763
 Calculate the area of an isosceles trapezoid ABCD, whose longer base measures 48 cm, the shorter base measures 3/4 of the longest base, and the leg of the trapezoid measures 2/3 of the longer base. The result is rounded to the nearest hundredth.
Calculate the area of an isosceles trapezoid ABCD, whose longer base measures 48 cm, the shorter base measures 3/4 of the longest base, and the leg of the trapezoid measures 2/3 of the longer base. The result is rounded to the nearest hundredth. - Rhombus
 One angle of a rhombus is 136°, and the shorter diagonal is 8 cm long. Find the length of the longer diagonal and the side of the rhombus.
One angle of a rhombus is 136°, and the shorter diagonal is 8 cm long. Find the length of the longer diagonal and the side of the rhombus. - R triangle
 Calculate the right triangle area whose longer leg is 6 dm shorter than the hypotenuse and 3 dm longer than the shorter leg.
Calculate the right triangle area whose longer leg is 6 dm shorter than the hypotenuse and 3 dm longer than the shorter leg. - The ladder - RT
 The ladder 16 feet reaches up 14 feet on a house wall. The 90-degree angle at the base of the house and wall. What are the other two angles or the length of the leg of the yard?
The ladder 16 feet reaches up 14 feet on a house wall. The 90-degree angle at the base of the house and wall. What are the other two angles or the length of the leg of the yard?
- Determine 18223
 From the sine theorem, determine the ratio of the sides of a triangle whose angles are 30 °, 60 °, and 90 °.
From the sine theorem, determine the ratio of the sides of a triangle whose angles are 30 °, 60 °, and 90 °. - Mr. Tolentino
 Mr. Tolentino owns a piece of land it measures 86.12 meters long and 68.293 meters in width. How much longer is the length than the width?
Mr. Tolentino owns a piece of land it measures 86.12 meters long and 68.293 meters in width. How much longer is the length than the width? - A rhombus 4
 A rhombus has a side length of 10 cm. Find the angles at each corner of the rhombus if the shorter of the two diagonals measures 7 cm. Give your answers to the nearest degree and give clear geometric reasoning at each stage of your solution.
A rhombus has a side length of 10 cm. Find the angles at each corner of the rhombus if the shorter of the two diagonals measures 7 cm. Give your answers to the nearest degree and give clear geometric reasoning at each stage of your solution. - The sum 11
 The sum of the measures of the two angles is 89°. One angle has a measure of 64°. What is the measure in degrees of the second angle?
The sum of the measures of the two angles is 89°. One angle has a measure of 64°. What is the measure in degrees of the second angle? - RT area
 A right triangle has an area of 54cm². Calculate the sizes of both legs if the shorter leg is 75% of the size of the longer leg.
A right triangle has an area of 54cm². Calculate the sizes of both legs if the shorter leg is 75% of the size of the longer leg.
- One angle 2
 One angle of a triangle measures 50°. The other two angles are in a ratio of 5:8. What are the measures of those two angles?
One angle of a triangle measures 50°. The other two angles are in a ratio of 5:8. What are the measures of those two angles? - Squares above sides
 In a right triangle, the areas of the squares above its sides are 169, 25, and 144. The length of its longer leg is:
In a right triangle, the areas of the squares above its sides are 169, 25, and 144. The length of its longer leg is: - Rectangle - sides
 A rectangle has an area 266 cm². The length of the shorter side is 5 cm fewer than the length of the longer side. What is the perimeter of a rectangle?
A rectangle has an area 266 cm². The length of the shorter side is 5 cm fewer than the length of the longer side. What is the perimeter of a rectangle? - Right trapezoid
 The right trapezoid has bases 3.2 cm and 62 mm long. The shorter leg has a length of 0.25 dm. Calculate the lengths of the diagonals and the second leg.
The right trapezoid has bases 3.2 cm and 62 mm long. The shorter leg has a length of 0.25 dm. Calculate the lengths of the diagonals and the second leg. - Parallelogram
 The perimeter of the parallelogram is 190 cm. The length of one side is 1.3-times longer than the length of the shorter side. What is the length of the sides of a parallelogram?
The perimeter of the parallelogram is 190 cm. The length of one side is 1.3-times longer than the length of the shorter side. What is the length of the sides of a parallelogram?
- Angles in a triangle
 In a triangle, the first angle measures a number plus 45°, and the second angle is 30° less than the first angle. The third angle is two times the number more than the first angle. What are the measurements of each angle of the triangle?
In a triangle, the first angle measures a number plus 45°, and the second angle is 30° less than the first angle. The third angle is two times the number more than the first angle. What are the measurements of each angle of the triangle? - Triangles
 Find out whether the given sizes of the angles can be interior angles of a triangle: a) 23°10',84°30',72°20' b) 90°,41°33',48°37' c) 14°51',90°,75°49' d) 58°58',59°59',60°3'
Find out whether the given sizes of the angles can be interior angles of a triangle: a) 23°10',84°30',72°20' b) 90°,41°33',48°37' c) 14°51',90°,75°49' d) 58°58',59°59',60°3' - Decorative 11881
 Mrs. Koláčkova wants to decorate the walls of her room with a strip of wallpaper 5 cm wide. How many meters of this decorative strip will he have to buy if the shorter side of the room measures 3 m and the longer side measures twice as much?
Mrs. Koláčkova wants to decorate the walls of her room with a strip of wallpaper 5 cm wide. How many meters of this decorative strip will he have to buy if the shorter side of the room measures 3 m and the longer side measures twice as much?
