Elevator
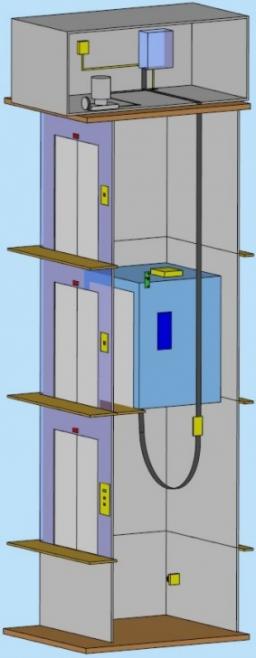
In homes with more floors, elevators are used. For passenger transport, the most commonly used traction elevator counterweight. The top of the shaft
engine room with the engine. The car is suspended on a rope, which is guided up over two pulleys to the counterweight.
Consider lift-enabled load Mmax = 300 kg
car weight mk = 500 kg
weight counterweight mz = 650 kg. The cabin moves at the speed
v0 = 1.2 m/s. The total efficiency of power is k =75%.
a) Explain what affects the efficiency of the system and the reason for using a counterweight.
b) Determine the power P1 engine lift if you summon empty cabin residents of the upper floors, which moves down the speed of v0.
c) Determine the power P2 engine lift when a group of citizens with a total mass M = 250 kg conveys speed v0 upwards.
In which of these cases b), c) the need for more power?
g = gravitational constant 10 N/kg
engine room with the engine. The car is suspended on a rope, which is guided up over two pulleys to the counterweight.
Consider lift-enabled load Mmax = 300 kg
car weight mk = 500 kg
weight counterweight mz = 650 kg. The cabin moves at the speed
v0 = 1.2 m/s. The total efficiency of power is k =75%.
a) Explain what affects the efficiency of the system and the reason for using a counterweight.
b) Determine the power P1 engine lift if you summon empty cabin residents of the upper floors, which moves down the speed of v0.
c) Determine the power P2 engine lift when a group of citizens with a total mass M = 250 kg conveys speed v0 upwards.
In which of these cases b), c) the need for more power?
g = gravitational constant 10 N/kg
Correct answer:
Tips for related online calculators
Our percentage calculator will help you quickly calculate various typical tasks with percentages.
Do you want to convert velocity (speed) units?
Do you want to convert time units like minutes to seconds?
Do you want to convert velocity (speed) units?
Do you want to convert time units like minutes to seconds?
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Themes, topics:
Grade of the word problem:
Related math problems and questions:
- Kangaroo 82979
 A kangaroo can move at a speed of 65 km/h. How many minutes will it take to move at this speed to a place 6500 m away?
A kangaroo can move at a speed of 65 km/h. How many minutes will it take to move at this speed to a place 6500 m away? - Tom can
 Tom can run 3/4 of a mile in 1/8 of an hour. What is the unit rate in miles per hour?
Tom can run 3/4 of a mile in 1/8 of an hour. What is the unit rate in miles per hour? - Noel drives
 Noel drives at an average speed of 52 miles per hour (mi/h) for 3 1/4 hours. How far has he traveled for 3 1/4 hours?
Noel drives at an average speed of 52 miles per hour (mi/h) for 3 1/4 hours. How far has he traveled for 3 1/4 hours? - An airplane 3
 An airplane descends at a rate of 2,700 feet per minute. Once the airplane starts its descent, what will be its elevation, in feet, after 3 1/5 minutes?
An airplane descends at a rate of 2,700 feet per minute. Once the airplane starts its descent, what will be its elevation, in feet, after 3 1/5 minutes? - Feed rate
 The feed rate of a drill is the distance it advances with each revolution. If a drill makes 320 rpm and drills a hole 2.625 inches deep in 1.8 minutes, what is the feed rate?
The feed rate of a drill is the distance it advances with each revolution. If a drill makes 320 rpm and drills a hole 2.625 inches deep in 1.8 minutes, what is the feed rate? - Water 71
 Water was heated to 80°c then allowed to cool at a rate of 6°c per minute. After how long was the temperature 8°C?
Water was heated to 80°c then allowed to cool at a rate of 6°c per minute. After how long was the temperature 8°C? - Lightning strike
 In a thunderstorm, the formula M=t/5.3 gives the approximate distance, M, in miles, from a lightning strike if it takes t second to hear the thunder after seeing the lightning. If you are 5.4 miles away from the lightning flash, how long will it take the
In a thunderstorm, the formula M=t/5.3 gives the approximate distance, M, in miles, from a lightning strike if it takes t second to hear the thunder after seeing the lightning. If you are 5.4 miles away from the lightning flash, how long will it take the - Balloon
 If a ceiling balloon rises at 120 m (about 400 ft) each minute, what is the ceiling of an overcast deck of stratus clouds 1500 m (about 5000 ft) thick if the balloon disappears into the clouds in 5 minutes? Show your solution.
If a ceiling balloon rises at 120 m (about 400 ft) each minute, what is the ceiling of an overcast deck of stratus clouds 1500 m (about 5000 ft) thick if the balloon disappears into the clouds in 5 minutes? Show your solution. - Konrad
 Konrad coaches football. He cycles 3 km to the stadium at an average 12 km/h speed. How long does Konrad take to cycle to the stadium?
Konrad coaches football. He cycles 3 km to the stadium at an average 12 km/h speed. How long does Konrad take to cycle to the stadium? - The temperature 45
 The temperature in a field is 68°F at 4 PM. The temperature decreases by 4°F per hour. When will the temperature be 60°F?
The temperature in a field is 68°F at 4 PM. The temperature decreases by 4°F per hour. When will the temperature be 60°F? - Water level
 Between 9 PM and 6:36 AM, the water level in a swimming pool decreased by 6/35. Assuming that the water level decreased at a constant rate, how much did the water level drop each hour?
Between 9 PM and 6:36 AM, the water level in a swimming pool decreased by 6/35. Assuming that the water level decreased at a constant rate, how much did the water level drop each hour? - The temperature 39
 The temperature outside is currently 10 degrees, dropping at an average rate of 2 degrees per hour. If the temperature continues to drop at this rate, what will the temperature be in 7 hours?
The temperature outside is currently 10 degrees, dropping at an average rate of 2 degrees per hour. If the temperature continues to drop at this rate, what will the temperature be in 7 hours? - Coefficient 81094
 A car moves along a horizontal road at a speed of 15 m/s. After turning off the engine, the car traveled a distance of 225 m. What was the coefficient of friction for this motion?
A car moves along a horizontal road at a speed of 15 m/s. After turning off the engine, the car traveled a distance of 225 m. What was the coefficient of friction for this motion? - Zendaya
 Zendaya walked 6 miles in 5 hours. What was her walking rate in hours per mile?
Zendaya walked 6 miles in 5 hours. What was her walking rate in hours per mile? - Destination 80553
 The train traveled along the high-speed line at an average speed of 180 km/h. He left the starting station at 6:00 a.m. and arrived at the destination at 8:40 a.m. But halfway through the journey, he stopped at the station, where he stood for 10 minutes.
The train traveled along the high-speed line at an average speed of 180 km/h. He left the starting station at 6:00 a.m. and arrived at the destination at 8:40 a.m. But halfway through the journey, he stopped at the station, where he stood for 10 minutes. - Home is home
 At 65km/h, Alfred can reach home in 50 minutes. At what speed should he drive his car so that he can reach home 10 minutes earlier?
At 65km/h, Alfred can reach home in 50 minutes. At what speed should he drive his car so that he can reach home 10 minutes earlier? - Minutes 80094
 Five hundred liters of water will flow into the pool in 5 minutes, and 120 liters of water will flow out of it in 12 minutes. How many liters of water will be added in 1 hour?
Five hundred liters of water will flow into the pool in 5 minutes, and 120 liters of water will flow out of it in 12 minutes. How many liters of water will be added in 1 hour?
