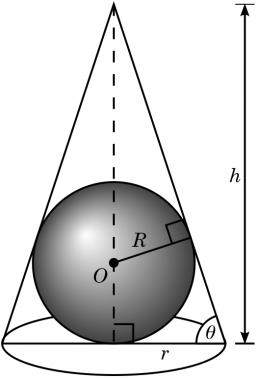
Sphere in cone
A sphere of radius 3 cm describes a cone with minimum volume. Determine cone dimensions.
Correct answer:
Tips for related online calculators
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
Tip: Our volume units converter will help you convert volume units.
Most natural application of trigonometry and trigonometric functions is a calculation of the triangles. Common and less common calculations of different types of triangles offers our triangle calculator. Word trigonometry comes from Greek and literally means triangle calculation.
Tip: Our volume units converter will help you convert volume units.
Most natural application of trigonometry and trigonometric functions is a calculation of the triangles. Common and less common calculations of different types of triangles offers our triangle calculator. Word trigonometry comes from Greek and literally means triangle calculation.
You need to know the following knowledge to solve this word math problem:
- algebra
- equation
- solid geometry
- cone
- sphere
- basic functions
- minimum
- derivation
- goniometry and trigonometry
- sine
- cosine
- tangent
- arccosine
Units of physical quantities:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Cone-shaped 82466
 The cone-shaped glass has a volume of 2.5 dl and a diameter of 13 cm. How much cocktail is left in the glass if the level only reaches half the height of the glass?
The cone-shaped glass has a volume of 2.5 dl and a diameter of 13 cm. How much cocktail is left in the glass if the level only reaches half the height of the glass? - A lamp
 A lamp shade like that of a frustum has a height of 12 cm and an upper and lower diameter of 10 cm and 20 cm. What area of materials is required to cover the curved surface of the frustum?
A lamp shade like that of a frustum has a height of 12 cm and an upper and lower diameter of 10 cm and 20 cm. What area of materials is required to cover the curved surface of the frustum? - A cone 3
 A cone has a diameter of x cm and a slant height of y cm. A square pyramid has a base side length of x cm and a slant height of y cm. Which has the greater surface area? Explain.
A cone has a diameter of x cm and a slant height of y cm. A square pyramid has a base side length of x cm and a slant height of y cm. Which has the greater surface area? Explain. - A Pile of salt
 A Pile of salt has been stored in the shape of a cone. Mr. Terwilliker knows that the pile is 20 feet tall and 102 feet in circumference at the base. What area of the conical tarpaulin (a large sheet of material) is needed to cover the pile?
A Pile of salt has been stored in the shape of a cone. Mr. Terwilliker knows that the pile is 20 feet tall and 102 feet in circumference at the base. What area of the conical tarpaulin (a large sheet of material) is needed to cover the pile? - The radius
 A right circular cone's radius and slant heights are 9 cm and 15 cm, respectively. Find, correct to one decimal place, the (i) Height (ii) Volume of the cone
A right circular cone's radius and slant heights are 9 cm and 15 cm, respectively. Find, correct to one decimal place, the (i) Height (ii) Volume of the cone - A cone 2
 A cone has a slant height of 10 cm and a square curved surface area of 50 pi cm. Find the base radius of the cone.
A cone has a slant height of 10 cm and a square curved surface area of 50 pi cm. Find the base radius of the cone. - An Elizabethan collar
 An Elizabethan collar is used to prevent an animal from irritating a wound. The angle between the opening (diameter 6 inches) with a 16-inch diameter and the side of the collar is 53 degrees. Find the surface area of the collar shown.
An Elizabethan collar is used to prevent an animal from irritating a wound. The angle between the opening (diameter 6 inches) with a 16-inch diameter and the side of the collar is 53 degrees. Find the surface area of the collar shown. - The diameter 4
 The cone's diameter is 14ft, and the height is 7 ft. What is the slant height?
The cone's diameter is 14ft, and the height is 7 ft. What is the slant height? - Angle of the sector
 Find the angle of the sector of a circle radius of 20 units where the area is equal to the lateral area of a cone with a radius of 8 units.
Find the angle of the sector of a circle radius of 20 units where the area is equal to the lateral area of a cone with a radius of 8 units. - Right-angled trapezoid
 A right-angled trapezoid with the measure of the acute angle of 50° is given. The lengths of its bases are 4 and 6 units. The volume of the solid obtained by rotation of the given trapezoid about the longer base is:
A right-angled trapezoid with the measure of the acute angle of 50° is given. The lengths of its bases are 4 and 6 units. The volume of the solid obtained by rotation of the given trapezoid about the longer base is: - Sphere submerged in the cone
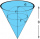 A right circular cone with a top width of 24 cm and an altitude of 8 cm is filled with water. A spherical steel ball with a radius of 3.0cm is submerged in the cone. Find the volume of water below the sphere.
A right circular cone with a top width of 24 cm and an altitude of 8 cm is filled with water. A spherical steel ball with a radius of 3.0cm is submerged in the cone. Find the volume of water below the sphere. - Similar frustums
 The upper and lower radii of a frustum of a right circular cone are 8 cm and 32 cm, respectively. If the altitude of the frustum is 10 cm, how far from the bottom base must a cutting plane be made to form two similar frustums?
The upper and lower radii of a frustum of a right circular cone are 8 cm and 32 cm, respectively. If the altitude of the frustum is 10 cm, how far from the bottom base must a cutting plane be made to form two similar frustums? - A cone
 A cone measures 6 inches in diameter at the base. The distance from the edge of the circumference to the top is 12 inches. Find its volume.
A cone measures 6 inches in diameter at the base. The distance from the edge of the circumference to the top is 12 inches. Find its volume. - An equilateral cone
 Determine the radius and height (in centimeters) of an equilateral cone that has a volume of 1 liter.
Determine the radius and height (in centimeters) of an equilateral cone that has a volume of 1 liter. - The conical roof
 The conical roof above the warehouse has a diameter of the lower part (base) d = 11.2 m and a height v = 3.3 m. How many rectangular steel plates with dimensions of 1.4 m and 0.9 m were needed to produce this roof if the seams and waste required an increa
The conical roof above the warehouse has a diameter of the lower part (base) d = 11.2 m and a height v = 3.3 m. How many rectangular steel plates with dimensions of 1.4 m and 0.9 m were needed to produce this roof if the seams and waste required an increa - Cone-shaped 47363
 We built a cone-shaped shelter with a base diameter of 4 m on the children's playground. Calculate the cone shell if the side of the cone measures 8 m
We built a cone-shaped shelter with a base diameter of 4 m on the children's playground. Calculate the cone shell if the side of the cone measures 8 m - Frustrum - volume, area
 Calculate the surface and volume of a truncated rotating cone with base radii of 8 cm and 4 cm and a height of 5 cm.
Calculate the surface and volume of a truncated rotating cone with base radii of 8 cm and 4 cm and a height of 5 cm.
