Sphere
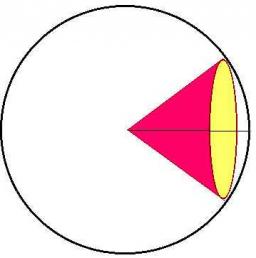
Intersect between the plane and a sphere is a circle with a radius of 60 mm. The cone, whose base is this circle and whose apex is at the center of the sphere, has a height of 34 mm. Calculate the surface area and volume of a sphere.
Correct answer:
Tips for related online calculators
Tip: Our volume units converter will help you convert volume units.
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Intersection 40981
 The intersection of a plane is 2 cm from the sphere's center, and this sphere is a circle whose radius is 6 cm. Calculate the surface area and volume of the sphere.
The intersection of a plane is 2 cm from the sphere's center, and this sphere is a circle whose radius is 6 cm. Calculate the surface area and volume of the sphere. - Surface and volume
 Calculate the surface and volume of a cylinder whose height is 8 dm and the radius of the base circle is 2 dm.
Calculate the surface and volume of a cylinder whose height is 8 dm and the radius of the base circle is 2 dm. - Calculate 5789
 Calculate the volume and surface of the rotating cone with the base radius r = 4.6dm and the height v = 230mm.
Calculate the volume and surface of the rotating cone with the base radius r = 4.6dm and the height v = 230mm. - One-quarter 46001
 Express in square centimeters the surface of a sphere whose radius is equal to one-quarter of the radius of the cone. The diameter of the base of the cone is 20 cm.
Express in square centimeters the surface of a sphere whose radius is equal to one-quarter of the radius of the cone. The diameter of the base of the cone is 20 cm.
- Calculate 32281
 The rotating cone has a base radius r = 226mm, and the deviation of the side from the base plane is 56 °. Calculate the height of the cone.
The rotating cone has a base radius r = 226mm, and the deviation of the side from the base plane is 56 °. Calculate the height of the cone. - Rotary cone
 A rotary cone whose height is equal to the circumference of the base has a volume 229 cm³. Calculate the radius of the base circle and the height of the cone.
A rotary cone whose height is equal to the circumference of the base has a volume 229 cm³. Calculate the radius of the base circle and the height of the cone. - Sphere cuts
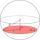 At what distance from the center intersects the sphere with radius R = 91 plane if the cut area and area of the main sphere circle are in ratio 3/6?
At what distance from the center intersects the sphere with radius R = 91 plane if the cut area and area of the main sphere circle are in ratio 3/6? - Cut and cone
 Calculate the volume of the rotation cone whose lateral surface is a circular arc with radius 15 cm and central angle 63 degrees.
Calculate the volume of the rotation cone whose lateral surface is a circular arc with radius 15 cm and central angle 63 degrees. - Rotating cone
 Calculate the volume and the surface area of a rotating cone of base radius r = 2.3 dm and a height h = 46 mm.
Calculate the volume and the surface area of a rotating cone of base radius r = 2.3 dm and a height h = 46 mm.
- Angle of deviation
 The surface of the rotating cone is 30 cm² (with a circle base), and its surface area is 20 cm². Calculate the deviation of this cone's side from the base's plane.
The surface of the rotating cone is 30 cm² (with a circle base), and its surface area is 20 cm². Calculate the deviation of this cone's side from the base's plane. - Cylinder - basics
 Cylinder with base radius r = 54 cm and height h=35 cm. Calculate: a) Area of the base
Cylinder with base radius r = 54 cm and height h=35 cm. Calculate: a) Area of the base - Cone
 The circular cone has height h = 29 dm and base radius r = 3 dm slice plane parallel to the base. Calculate the distance of the cone vertex from this plane if solids have the same volume.
The circular cone has height h = 29 dm and base radius r = 3 dm slice plane parallel to the base. Calculate the distance of the cone vertex from this plane if solids have the same volume. - A spherical segment
 The aspherical section, whose axial section has an angle of j = 120° in the center of the sphere, is part of a sphere with a radius r = 10 cm. Calculate the cut surface.
The aspherical section, whose axial section has an angle of j = 120° in the center of the sphere, is part of a sphere with a radius r = 10 cm. Calculate the cut surface. - Cone side
 Calculate the volume and area of the cone whose height is 10 cm, and the axial section of the cone has an angle of 30 degrees between height and the cone side.
Calculate the volume and area of the cone whose height is 10 cm, and the axial section of the cone has an angle of 30 degrees between height and the cone side.
- Circular 4690
 The cone shell with a base radius of 20 cm and a height of 50 cm unfolds into a circular cutout. How big is the center angle of this cutout?
The cone shell with a base radius of 20 cm and a height of 50 cm unfolds into a circular cutout. How big is the center angle of this cutout? - Deviation 70744
 Calculate the volume and surface of the rotating cone if its height is 10 cm and the side has a deviation of 30 ° from the base plane.
Calculate the volume and surface of the rotating cone if its height is 10 cm and the side has a deviation of 30 ° from the base plane. - Determine 82032
 Determine the volume and surface area of a cone whose slope of length 8 cm makes an angle of 75 degrees with the plane of the base.
Determine the volume and surface area of a cone whose slope of length 8 cm makes an angle of 75 degrees with the plane of the base.
