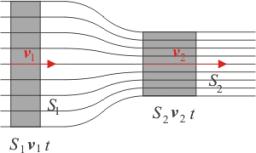
Velocity ratio
Determine the ratio at which the fluid velocity in different parts of the pipeline (one piece has a diameter of 5 cm and the other has a diameter of 3 cm) when you know that every point of the liquid is the product of the area of the tube [S] and the fluid velocity [v] the same.
Correct answer:
Tips for related online calculators
Check out our ratio calculator.
Tip: Our volume units converter will help you convert volume units.
Do you want to convert velocity (speed) units?
Do you want to convert time units like minutes to seconds?
Tip: Our volume units converter will help you convert volume units.
Do you want to convert velocity (speed) units?
Do you want to convert time units like minutes to seconds?
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Themes, topics:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Rectangular 2885
 A total of ten exhibitors gathered at the long-haired cat show. It was exhibited in a rectangular room with two rows of tables as shown. The cats were marked with different numbers from 1 to 10, and one cat sat on each table. Determine which cat was rated
A total of ten exhibitors gathered at the long-haired cat show. It was exhibited in a rectangular room with two rows of tables as shown. The cats were marked with different numbers from 1 to 10, and one cat sat on each table. Determine which cat was rated - Rubberized 19963
 The circular pool with a diameter of 3.5 m is covered with a circular tarpaulin made of rubberized fabric for CZK 110 per square meter. Determine how much the tarpaulin cost if you know that its radius is 25 cm larger than the radius of the pool.
The circular pool with a diameter of 3.5 m is covered with a circular tarpaulin made of rubberized fabric for CZK 110 per square meter. Determine how much the tarpaulin cost if you know that its radius is 25 cm larger than the radius of the pool. - MIT 1869
 You know the length of hypotenuse parts 9 and 16, at which the hypotenuse of a right triangle is divided by a height. The task is to find the lengths of the sides of the triangle and the length of line x. This assignment was part of the Massachusetts Inst
You know the length of hypotenuse parts 9 and 16, at which the hypotenuse of a right triangle is divided by a height. The task is to find the lengths of the sides of the triangle and the length of line x. This assignment was part of the Massachusetts Inst - Circumference 82489
 An isosceles trapezoid has one base twice as short as the other. Its content is 42cm², and its height is 4cm. Calculate its circumference if you know that the arm is 5.3 cm long.
An isosceles trapezoid has one base twice as short as the other. Its content is 42cm², and its height is 4cm. Calculate its circumference if you know that the arm is 5.3 cm long. - Perpendicular projection
 Determine the distance of a point B[1, -3] from the perpendicular projection of a point A[3, -2] on a straight line 2 x + y + 1 = 0.
Determine the distance of a point B[1, -3] from the perpendicular projection of a point A[3, -2] on a straight line 2 x + y + 1 = 0. - A Cartesian framework
 1. In a Cartesian framework, the functions f and g we know that: The function (f) is defined by f (x) = 2x², the function (g) is defined by g (x) = x + 3, the point (O) is the origin of the reference, and point (C) is the point of intersection of the grap
1. In a Cartesian framework, the functions f and g we know that: The function (f) is defined by f (x) = 2x², the function (g) is defined by g (x) = x + 3, the point (O) is the origin of the reference, and point (C) is the point of intersection of the grap - On line
 On line p: x = 4 + t, y = 3 + 2t, t is R, find point C, which has the same distance from points A [1,2] and B [-1,0].
On line p: x = 4 + t, y = 3 + 2t, t is R, find point C, which has the same distance from points A [1,2] and B [-1,0]. - Coordinates of square vertices
 The ABCD square has the center S [−3, −2] and the vertex A [1, −3]. Find the coordinates of the other vertices of the square.
The ABCD square has the center S [−3, −2] and the vertex A [1, −3]. Find the coordinates of the other vertices of the square. - Transport 39383
 The online store offers free shipping when you buy five or more products. The price of transport is 100 crowns. When you buy five products without shipping, we pay the same amount as when you buy three products with shipping included. How much does 1 piec
The online store offers free shipping when you buy five or more products. The price of transport is 100 crowns. When you buy five products without shipping, we pay the same amount as when you buy three products with shipping included. How much does 1 piec - Pipeline
 How much percent has changed (reduced) the pipe cross-section area if the circular shape changed to square with the same perimeter?
How much percent has changed (reduced) the pipe cross-section area if the circular shape changed to square with the same perimeter? - Parametric form
 Calculate the distance of point A [2,1] from the line p: X = -1 + 3 t Y = 5-4 t Line p has a parametric form of the line equation.
Calculate the distance of point A [2,1] from the line p: X = -1 + 3 t Y = 5-4 t Line p has a parametric form of the line equation. - Tissues
 The store got three kinds of tissues - 132 children, 156 women, and 204 men. Tissues for each species were packed into boxes after the number of pieces was the same for all three types (and greatest). Determine the number if you know that every box has mo
The store got three kinds of tissues - 132 children, 156 women, and 204 men. Tissues for each species were packed into boxes after the number of pieces was the same for all three types (and greatest). Determine the number if you know that every box has mo - Axial section of the cone
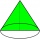 The axial section of the cone is an isosceles triangle in which the ratio of cone diameter to cone side is 2:3. Calculate its volume if you know its area is 314 cm square.
The axial section of the cone is an isosceles triangle in which the ratio of cone diameter to cone side is 2:3. Calculate its volume if you know its area is 314 cm square. - Midnight 67644
 The bacteria in the test tube divide into two every second, with each new one having the same volume as the original. At exactly midnight, the test tube was full. At what time was the test tube half full?
The bacteria in the test tube divide into two every second, with each new one having the same volume as the original. At exactly midnight, the test tube was full. At what time was the test tube half full? - Direct route
 From two different places A and B, connected by a direct route, Adam (from city A) and Bohus (from city B) started at a constant speed. As Adam continued to go from A to B, Bohus turned around at the time of their meeting, and at the same speed, he return
From two different places A and B, connected by a direct route, Adam (from city A) and Bohus (from city B) started at a constant speed. As Adam continued to go from A to B, Bohus turned around at the time of their meeting, and at the same speed, he return - Fraction and ratios
 Fraction and ratios are different names for the same thing.
Fraction and ratios are different names for the same thing. - Daily temperature
 The average daily temperature measurements for one week every day at the same hour was -2.8 °C. We measured all temperatures on different days are different. The highest daily maximum temperature was 2.4 °C, and the lowest was -6 °C. Determine the options
The average daily temperature measurements for one week every day at the same hour was -2.8 °C. We measured all temperatures on different days are different. The highest daily maximum temperature was 2.4 °C, and the lowest was -6 °C. Determine the options
