Bearing - navigation
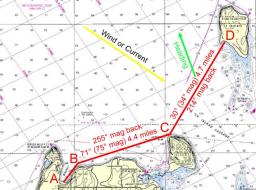
A ship travels 84 km on a bearing of 17° and then travels on a bearing of 107° for 135 km. Find the distance of the end of the trip from the starting point to the nearest kilometer.
Correct answer:
Showing 3 comments:
Dr Math
Q: A ship sailing on a bearing of 090⁰, its direction is?
A: A bearing of 90° is direction to the east.
north representing 0° or 360°
east representing 90°
south representing 180°
west representing 270°
A: A bearing of 90° is direction to the east.
north representing 0° or 360°
east representing 90°
south representing 180°
west representing 270°
2 years ago 1 Like
Tips for related online calculators
Our vector sum calculator can add two vectors given by their magnitudes and by included angle.
The Pythagorean theorem is the base for the right triangle calculator.
Do you want to round the number?
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
The Pythagorean theorem is the base for the right triangle calculator.
Do you want to round the number?
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
You need to know the following knowledge to solve this word math problem:
- geometry
- vector
- arithmetic
- square root
- rounding
- planimetrics
- Pythagorean theorem
- triangle
- goniometry and trigonometry
- sine
- cosine
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Plane II
 A plane flew 50 km on a bearing of 63°20' and then flew in the direction of 153°20' for 140km. Find the distance between the starting point and the ending point.
A plane flew 50 km on a bearing of 63°20' and then flew in the direction of 153°20' for 140km. Find the distance between the starting point and the ending point. - Airport's 80482
 The plane flew from airport m on a course of 132° to airport n, then from n to p on a course of 235°. The distance between the airport's mn is 380 km, np 284 km. What will be the return course to m, and what is the distance between the airport's pm?
The plane flew from airport m on a course of 132° to airport n, then from n to p on a course of 235°. The distance between the airport's mn is 380 km, np 284 km. What will be the return course to m, and what is the distance between the airport's pm? - In the desert
 A man wondering in the desert walks 5.7 miles in the direction S 26° W. He then turns 90° and walks 9 miles in the direction N 49° W. At that time, how far is he from his starting point, and what is his bearing from his starting point?
A man wondering in the desert walks 5.7 miles in the direction S 26° W. He then turns 90° and walks 9 miles in the direction N 49° W. At that time, how far is he from his starting point, and what is his bearing from his starting point? - A boy 5
 A boy starts at A and walks 3km east to B. He then walks 4km north to C. Find the bearing of C from A.
A boy starts at A and walks 3km east to B. He then walks 4km north to C. Find the bearing of C from A. - Aircraft bearing
 Two aircraft will depart from the airport simultaneously. The first flight flies with a course of 30°, and the second with a course of 86°. Both fly at 330 km/h. How far apart will they be in 45 minutes of flight?
Two aircraft will depart from the airport simultaneously. The first flight flies with a course of 30°, and the second with a course of 86°. Both fly at 330 km/h. How far apart will they be in 45 minutes of flight? - A hiker
 A hiker plans to hike up one side of a mountain and down the other side of points a mountain, each side of the mountain formed by a straight line. The angle of elevation at the starting point is 42.4 degrees, and the angle of elevation at the end is 48.3
A hiker plans to hike up one side of a mountain and down the other side of points a mountain, each side of the mountain formed by a straight line. The angle of elevation at the starting point is 42.4 degrees, and the angle of elevation at the end is 48.3 - A radio antenna
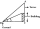 Avanti is trying to find the height of a radio antenna on the roof of a local building. She stands at a horizontal distance of 21 meters from the building. The angle of elevation from her eyes to the roof (point A) is 42°, and the angle of elevation from
Avanti is trying to find the height of a radio antenna on the roof of a local building. She stands at a horizontal distance of 21 meters from the building. The angle of elevation from her eyes to the roof (point A) is 42°, and the angle of elevation from - Expressway 5837
 The expressway covers the distance from the starting point to the final station in 4 hours and 20 minutes. A passenger train, whose average speed is 30 km/h less, will cover this distance in 7 h 40 min. What is the speed of the express train, and what is
The expressway covers the distance from the starting point to the final station in 4 hours and 20 minutes. A passenger train, whose average speed is 30 km/h less, will cover this distance in 7 h 40 min. What is the speed of the express train, and what is - A ship
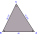 A ship has been spotted by two lighthouses, A and B, as shown in the figure. What is the distance from the ship to Lighthouse A to the nearest tenth? Figure - the distance between lighthouses A and B is 40 nautical miles. From A is seen in view angle 57°
A ship has been spotted by two lighthouses, A and B, as shown in the figure. What is the distance from the ship to Lighthouse A to the nearest tenth? Figure - the distance between lighthouses A and B is 40 nautical miles. From A is seen in view angle 57° - Hiking trip
 Rosie went on a hiking trip. On the first day, she walked 18 kilometers. Each day since she walked 90 percent of what she had walked the day before. What is the total distance Rosie has traveled by the end of the 10th day? Please round your final answer t
Rosie went on a hiking trip. On the first day, she walked 18 kilometers. Each day since she walked 90 percent of what she had walked the day before. What is the total distance Rosie has traveled by the end of the 10th day? Please round your final answer t - A man 7
 A man wandering in the desert walks 3.8 miles in the direction of S 44° W. He then turns and walks 2.2 miles in the direction of N 55° W. At that time, how far is he from his starting point? (Round your answer to two decimal places.)
A man wandering in the desert walks 3.8 miles in the direction of S 44° W. He then turns and walks 2.2 miles in the direction of N 55° W. At that time, how far is he from his starting point? (Round your answer to two decimal places.) - Perpendicular 17423
 According to the map, the scouts were supposed to proceed through the forest perpendicular to its straight edge, where the goal was 3 km away from the starting point. They already deviated from the correct direction by 5° at the start. How far from the ta
According to the map, the scouts were supposed to proceed through the forest perpendicular to its straight edge, where the goal was 3 km away from the starting point. They already deviated from the correct direction by 5° at the start. How far from the ta - Journey 5
 A man has to make a journey of 84km in 3 hours. He travels the first 30km at 20km/hr. At what rate must he travel the remaining distance to complete his journey on time?
A man has to make a journey of 84km in 3 hours. He travels the first 30km at 20km/hr. At what rate must he travel the remaining distance to complete his journey on time? - The ship
 The ship went at the upstream speed of 20 km/h in relation to water. The river flows at a speed of 10 km/h. After half an hour, he stopped and returned downstream to the starting point. How long does it take back when even if the downstream speed of the s
The ship went at the upstream speed of 20 km/h in relation to water. The river flows at a speed of 10 km/h. After half an hour, he stopped and returned downstream to the starting point. How long does it take back when even if the downstream speed of the s - The spacecraft
 The spacecraft spotted a radar device at an altitude angle alpha = 34 degrees 37 minutes and had a distance of u = 615km from Earth's observation point. Calculate the distance d of the spacecraft from Earth at the moment of observation. Earth is considere
The spacecraft spotted a radar device at an altitude angle alpha = 34 degrees 37 minutes and had a distance of u = 615km from Earth's observation point. Calculate the distance d of the spacecraft from Earth at the moment of observation. Earth is considere - Two ships
 The distance from A to B is 300km. At 7 AM started, from A to B, a ferry with speed higher by 20 km/h than a ship that leaves at 8 o'clock from B to A. Both met at 10:24. Find how far they will meet from A and when they will reach the destination.
The distance from A to B is 300km. At 7 AM started, from A to B, a ferry with speed higher by 20 km/h than a ship that leaves at 8 o'clock from B to A. Both met at 10:24. Find how far they will meet from A and when they will reach the destination. - Car
 The car goes from point A to point B at speed 86 km/h and back 53 km/h. If it goes there and back at speed 67 km/h trip would take 10 minutes shorter. What is the distance between points A and B?
The car goes from point A to point B at speed 86 km/h and back 53 km/h. If it goes there and back at speed 67 km/h trip would take 10 minutes shorter. What is the distance between points A and B?
