Two forces
Two forces with magnitudes of 25 and 30 pounds act on an object at 10° and 100° angles. Find the direction and magnitude of the resultant force. Round to two decimal places in all intermediate steps and your final answer.
Correct answer:
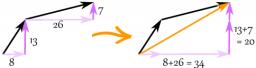
Showing 1 comment:
Dr Math
Angle 100-10 = 90° is right , therefore may be some optimization of calculation made. In general it§s calculated OK.
See also vector adding calculator:
https://www.hackmath.net/en/calculator/sum-of-the-two-vectors?a=25&a1=100-10&b=30&submit=Solve
See also vector adding calculator:
https://www.hackmath.net/en/calculator/sum-of-the-two-vectors?a=25&a1=100-10&b=30&submit=Solve
Tips for related online calculators
Our vector sum calculator can add two vectors given by their magnitudes and by included angle.
See also our right triangle calculator.
Do you want to round the number?
See also our trigonometric triangle calculator.
See also our right triangle calculator.
Do you want to round the number?
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
- geometry
- vector
- arithmetic
- rounding
- addition
- planimetrics
- Pythagorean theorem
- right triangle
- triangle
- goniometry and trigonometry
- sine
- cosine
- tangent
- arctangent
Units of physical quantities:
Themes, topics:
Grade of the word problem:
Related math problems and questions:
- EE school boarding
 Three vectors, A, B, and C, are related as follows: A/C = 2 at 120 deg, A + B = -5 + j15, C = conjugate of B. Find C.
Three vectors, A, B, and C, are related as follows: A/C = 2 at 120 deg, A + B = -5 + j15, C = conjugate of B. Find C. - Meridian ground speed
 The plane flies south at an average speed of 190 km/h, and the wind blows from west to east at a speed of 20 m/s. How fast and in what direction (relative to the meridian) will the plane move relative to the ground?
The plane flies south at an average speed of 190 km/h, and the wind blows from west to east at a speed of 20 m/s. How fast and in what direction (relative to the meridian) will the plane move relative to the ground? - Triangle 82
 Triangle PQR has vertices located at (2, 2), (5, -4), and (-4, -1). What type of triangle is triangle PQR?
Triangle PQR has vertices located at (2, 2), (5, -4), and (-4, -1). What type of triangle is triangle PQR? - Crosswind
 A plane is traveling 45 degrees N of E at 320 km/h when it comes across a current from S of E at 115 degrees of 20 km/h. What are the airplane's new course and speed?
A plane is traveling 45 degrees N of E at 320 km/h when it comes across a current from S of E at 115 degrees of 20 km/h. What are the airplane's new course and speed? - A triangle 6
 A triangle has vertices on a coordinate grid at H(-2,7), I(4,7), and J(4,-9). What is the length, in units, of vector HI?
A triangle has vertices on a coordinate grid at H(-2,7), I(4,7), and J(4,-9). What is the length, in units, of vector HI? - Raj walk
 Raj walks 9/7 km from place A towards the east and then from there 2 1/4 km towards the west. Where will he be now from A?
Raj walks 9/7 km from place A towards the east and then from there 2 1/4 km towards the west. Where will he be now from A? - North + west
 Find the magnitude of the resultant of the given vectors: vector 1:2 m/s, north vector 2:7 m/s, west
Find the magnitude of the resultant of the given vectors: vector 1:2 m/s, north vector 2:7 m/s, west - A man 7
 A man wandering in the desert walks 3.8 miles in the direction of S 44° W. He then turns and walks 2.2 miles in the direction of N 55° W. At that time, how far is he from his starting point? (Round your answer to two decimal places.)
A man wandering in the desert walks 3.8 miles in the direction of S 44° W. He then turns and walks 2.2 miles in the direction of N 55° W. At that time, how far is he from his starting point? (Round your answer to two decimal places.) - Designated 71874
 The patrol had started at a designated marching angle (an azimuth) of 13°. After 9 km, the azimuth's angle changed to 62°. The patrol went 10 km in this direction. Find the distance from where the patrol started.
The patrol had started at a designated marching angle (an azimuth) of 13°. After 9 km, the azimuth's angle changed to 62°. The patrol went 10 km in this direction. Find the distance from where the patrol started. - Calculate 66814
 Calculate the area and perimeter of the right triangle ABC if A [5.5; -2.5] B [-3; 5] C [-3; -2.5]
Calculate the area and perimeter of the right triangle ABC if A [5.5; -2.5] B [-3; 5] C [-3; -2.5] - Book Store
 The Mabini Book Store (MBS) is reducing the prices of Mathematics books for promotion. The store has 6 Algebra books, 6 Geometry books, and 5 Statistics books to be arranged on a shelf. Books of the same kind are to be placed beside each other. How many w
The Mabini Book Store (MBS) is reducing the prices of Mathematics books for promotion. The store has 6 Algebra books, 6 Geometry books, and 5 Statistics books to be arranged on a shelf. Books of the same kind are to be placed beside each other. How many w - Raindrops
 The car runs on a horizontal track at a constant speed of 20 m2-1. It is raining. Raindrops fall in a vertical direction at a speed of 6 m/s. a) How fast is the speed of the drops relative to the car windows? b) What is the angle of the raindro
The car runs on a horizontal track at a constant speed of 20 m2-1. It is raining. Raindrops fall in a vertical direction at a speed of 6 m/s. a) How fast is the speed of the drops relative to the car windows? b) What is the angle of the raindro - Three
 Three points are given: A (-3, 1), B (2, -4), C (3, 3) a) Find the perimeter of triangle ABC. b) Decide what type of triangle the triangle ABC is. c) Find the length of the inscribed circle
Three points are given: A (-3, 1), B (2, -4), C (3, 3) a) Find the perimeter of triangle ABC. b) Decide what type of triangle the triangle ABC is. c) Find the length of the inscribed circle - Vectors
 Find the magnitude of the angle between two vectors u = (3; -5) and v = (10; 6)
Find the magnitude of the angle between two vectors u = (3; -5) and v = (10; 6) - Lengths of medians from coordinates
 There is a triangle ABC: A [-6.6; 1.2], B [3.4; -5.6], C [2.8; 4.2]. Calculate the lengths of its medians.
There is a triangle ABC: A [-6.6; 1.2], B [3.4; -5.6], C [2.8; 4.2]. Calculate the lengths of its medians. - Angle ASB
 On a circle with a radius of 10 cm and with a center S, the points A, B, and C are given so that the central angle ASB is 60 degrees and the central angle ASC is 90 degrees. Find the length of the circular arc and the amount of AB and AC offsets.
On a circle with a radius of 10 cm and with a center S, the points A, B, and C are given so that the central angle ASB is 60 degrees and the central angle ASC is 90 degrees. Find the length of the circular arc and the amount of AB and AC offsets. - CoG center
 Find the position of the center of gravity of a system of four mass points having masses, m1, m2 = 2 m1, m3 = 3 m1, and m4 = 4 m1, if they lie at the vertices of an isosceles tetrahedron. (in all case
Find the position of the center of gravity of a system of four mass points having masses, m1, m2 = 2 m1, m3 = 3 m1, and m4 = 4 m1, if they lie at the vertices of an isosceles tetrahedron. (in all case
