Probability
In the lottery, numbers are drawn five from 50. What are the chances you will win the first prize?
Correct answer:

Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
Grade of the word problem:
Related math problems and questions:
- Hazard game
 In the Sportka hazard game, six numbers out of 49 are drawn. What is the probability that we will win: a) second prize (we guess five numbers correctly) b) the third prize (we guess four numbers correctly)?
In the Sportka hazard game, six numbers out of 49 are drawn. What is the probability that we will win: a) second prize (we guess five numbers correctly) b) the third prize (we guess four numbers correctly)? - Second prize
 Jamie and Mark each bought a raffle ticket to win a new laptop or a new cell phone, where only 125 tickets were told. The first ticket holder wins the prize of their choice and is removed from the drawing. The holder of the second ticket drawn wins the re
Jamie and Mark each bought a raffle ticket to win a new laptop or a new cell phone, where only 125 tickets were told. The first ticket holder wins the prize of their choice and is removed from the drawing. The holder of the second ticket drawn wins the re - Probability 5786
 There are 200 tickets in the raffle with one main prize. Miško bought 25 tickets. What is the probability that Miško will not win the main prize?
There are 200 tickets in the raffle with one main prize. Miško bought 25 tickets. What is the probability that Miško will not win the main prize? - Probability 17023
 In the draw pole, five numbers out of 35 are drawn. The third prize is paid for three guessed numbers. What is the probability of winning the third prize if we submit a ticket with one of five numbers?
In the draw pole, five numbers out of 35 are drawn. The third prize is paid for three guessed numbers. What is the probability of winning the third prize if we submit a ticket with one of five numbers?
- Probability - tickets
 What is the probability when you have 25 tickets in 5000 that you do not win the first (one) prize?
What is the probability when you have 25 tickets in 5000 that you do not win the first (one) prize? - Two prizes
 Teacher Mae is giving away a random prize to a class of 15 pupils (7 boys and eight girls). What is the probability that girls will win both prizes?
Teacher Mae is giving away a random prize to a class of 15 pupils (7 boys and eight girls). What is the probability that girls will win both prizes? - Win in raffle
 The raffle tickets were sold to 200, 5 of which were winning. What is the probability that Peter, who bought one ticket, will win?
The raffle tickets were sold to 200, 5 of which were winning. What is the probability that Peter, who bought one ticket, will win? - Lottery - eurocents
 Tereza bets in the lottery and finally wins. She went to the booth to have the prize paid out. An elderly gentleman beside him wants to buy a newspaper but is missing five cents. Tereza is in a generous mood after the win, so she gives the man five cents
Tereza bets in the lottery and finally wins. She went to the booth to have the prize paid out. An elderly gentleman beside him wants to buy a newspaper but is missing five cents. Tereza is in a generous mood after the win, so she gives the man five cents - Pet store 2
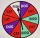 A pet store is having a prize giveaway. The spinner shows the type of toy a customer can win for their pet. If a customer spins the spinner and it lands on a cat, they will win a free cat toy. If the spinner is spun 540 times throughout the day, about how
A pet store is having a prize giveaway. The spinner shows the type of toy a customer can win for their pet. If a customer spins the spinner and it lands on a cat, they will win a free cat toy. If the spinner is spun 540 times throughout the day, about how
- Twenty-five 81187
 Twenty-five prizes are drawn in a raffle with 500 tickets. How many tickets do we need to buy to ensure I win at least 3 prizes?
Twenty-five prizes are drawn in a raffle with 500 tickets. How many tickets do we need to buy to ensure I win at least 3 prizes? - Friends 81380
 In the lottery, where 326 numbers are drawn, Maros marked 7 numbers on the ticket. Kamil marked 11 numbers in another lottery, and 421 numbers were drawn. Which of these friends has a better chance of winning?
In the lottery, where 326 numbers are drawn, Maros marked 7 numbers on the ticket. Kamil marked 11 numbers in another lottery, and 421 numbers were drawn. Which of these friends has a better chance of winning? - Guaranteed 37611
 Determine how many different ways a Lotto ticket can be written if we guess six numbers out of 49. At what Jackpot would it already pay to bet so many tickets to be guaranteed to win the 1st prize? The price of one type is €1.
Determine how many different ways a Lotto ticket can be written if we guess six numbers out of 49. At what Jackpot would it already pay to bet so many tickets to be guaranteed to win the 1st prize? The price of one type is €1. - Compare distributions
 Which would you expect to be larger, the standard deviation of 5 random numbers picked from 1 to 47 in the California Super Lotto (CSL - write 1 as a result), or the standard deviation of 5 random numbers picked from 1 to 69 in the multi-state PowerBall L
Which would you expect to be larger, the standard deviation of 5 random numbers picked from 1 to 47 in the California Super Lotto (CSL - write 1 as a result), or the standard deviation of 5 random numbers picked from 1 to 69 in the multi-state PowerBall L - Lottery
 Fernando has two lottery tickets, each from the other lottery. In the first is 973 000 lottery tickets from them wins 687 000, the second has 1425 000 lottery tickets from them wins 1425 000 tickets. What is the probability that at least one Fernando's ti
Fernando has two lottery tickets, each from the other lottery. In the first is 973 000 lottery tickets from them wins 687 000, the second has 1425 000 lottery tickets from them wins 1425 000 tickets. What is the probability that at least one Fernando's ti
- Entertainment 41081
 In the entertainment lottery, they draw one number from 1 to 35. What is the probability that they will draw an odd compound number?
In the entertainment lottery, they draw one number from 1 to 35. What is the probability that they will draw an odd compound number? - Probability 63434
 There are tickets with the numbers 1, 2, 3, 4, 5, 6, 7, and 8 in the envelope. Two tickets are drawn from the envelope at a time. What is the probability that the sum of the numbers drawn will be 7? Write the result as a decimal rounded to hundredths.
There are tickets with the numbers 1, 2, 3, 4, 5, 6, 7, and 8 in the envelope. Two tickets are drawn from the envelope at a time. What is the probability that the sum of the numbers drawn will be 7? Write the result as a decimal rounded to hundredths. - Contestants
 The three best contestants are to divide the total prize of CZK 4,200. The second gets 20% more than the third. And the first one gets 200 CZK less than the second and the third together. How much will everyone get?
The three best contestants are to divide the total prize of CZK 4,200. The second gets 20% more than the third. And the first one gets 200 CZK less than the second and the third together. How much will everyone get?
