Rectangle vs square
One side of the rectangle is 1 cm shorter than the side of the square. The second side is 3 cm longer than the side of the square. The square and rectangle have the same area. Calculate the length of the sides of a square and a rectangle.
Correct answer:
Tips for related online calculators
Looking for a statistical calculator?
Are you looking for help with calculating roots of a quadratic equation?
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
Are you looking for help with calculating roots of a quadratic equation?
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
You need to know the following knowledge to solve this word math problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Dimensions 83176
 If we reduce the length of the rectangle by 2 cm and the width by 1 cm, its area will decrease by 8 cm². If we increase the length of the rectangle by 1 cm and the width by 2 cm, then its content will increase by 13 cm². What were the original dimensions
If we reduce the length of the rectangle by 2 cm and the width by 1 cm, its area will decrease by 8 cm². If we increase the length of the rectangle by 1 cm and the width by 2 cm, then its content will increase by 13 cm². What were the original dimensions - Vertex of the rectangle
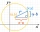 Determine the coordinates of the vertex of the rectangle inscribed in the circle x²+y² -2x-4y-20=0 if you know that one of its sides lies on the line p: x+2y=0
Determine the coordinates of the vertex of the rectangle inscribed in the circle x²+y² -2x-4y-20=0 if you know that one of its sides lies on the line p: x+2y=0 - Circle - analytics geometry
 Write the equation of the circle that passes through the points Q[3.5] R[2.6] and has its center on the line 2x+3y-4=0.
Write the equation of the circle that passes through the points Q[3.5] R[2.6] and has its center on the line 2x+3y-4=0. - Calculate 415
 Calculate the cuboid's dimensions if the sum of its edges is 19cm. The body's diagonal size is 13 cm, and its volume is 144 cm³. The total surface area is 192 cm².
Calculate the cuboid's dimensions if the sum of its edges is 19cm. The body's diagonal size is 13 cm, and its volume is 144 cm³. The total surface area is 192 cm².
- Parallelogram 79744
 A parallelogram has a perimeter of 30 cm and heights of 10 cm and 6 cm. Find the lengths of its sides.
A parallelogram has a perimeter of 30 cm and heights of 10 cm and 6 cm. Find the lengths of its sides. - Five friends
 Five friends ate a 12-slice pizza. Samir ate three times as many slices as Joe. Joe ate half as many slices as Emily. Kendra and Fong together ate half a pizza. Kendra ate one-third as many slices as Samir. Fong ate the most slices. What fraction of a piz
Five friends ate a 12-slice pizza. Samir ate three times as many slices as Joe. Joe ate half as many slices as Emily. Kendra and Fong together ate half a pizza. Kendra ate one-third as many slices as Samir. Fong ate the most slices. What fraction of a piz - Length 26
 The length of the median of the trapezoid is 10 inches. The median divides the trapezoid into two areas whose ratio is 3:5. The length of the shorter base is:
The length of the median of the trapezoid is 10 inches. The median divides the trapezoid into two areas whose ratio is 3:5. The length of the shorter base is: - The ratio 7
 The ratio of the sides of two squares is 4:5 if the sum of their areas is 180 cm². Find the sides of the two squares.
The ratio of the sides of two squares is 4:5 if the sum of their areas is 180 cm². Find the sides of the two squares. - 144 steps
 To get around the garden, we have to take 144 steps—eight steps less in width than in length. One step is five decimetres long. What are the dimensions of the garden? What are its perimeter and its area?
To get around the garden, we have to take 144 steps—eight steps less in width than in length. One step is five decimetres long. What are the dimensions of the garden? What are its perimeter and its area?
- Louis
 Louis wants to carpet the rectangular floor of his basement. The basement has an area of 5,120 square feet. The width of the basement is 4/5 its length. What is the length of Louis's basement?
Louis wants to carpet the rectangular floor of his basement. The basement has an area of 5,120 square feet. The width of the basement is 4/5 its length. What is the length of Louis's basement? - Truncated pyramid
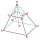 The truncated regular quadrilateral pyramid has a volume of 74 cm3, a height v = 6 cm, and an area of the lower base 15 cm² greater than the upper base's area. Calculate the area of the upper base.
The truncated regular quadrilateral pyramid has a volume of 74 cm3, a height v = 6 cm, and an area of the lower base 15 cm² greater than the upper base's area. Calculate the area of the upper base. - Harry
 Harry Thomson bought a large land in the shape of a rectangle with a circumference of 90 meters. He divided it into three rectangular plots. The shorter side has all three plots of equal length. Their longer sides are three consecutive natural numbers. Fi
Harry Thomson bought a large land in the shape of a rectangle with a circumference of 90 meters. He divided it into three rectangular plots. The shorter side has all three plots of equal length. Their longer sides are three consecutive natural numbers. Fi - Outside point
 The square ABCD and the point E lying outside the given square are given. What is the area of the square when the distance | AE | = 2, | DE | = 5 a | BE | = 4?
The square ABCD and the point E lying outside the given square are given. What is the area of the square when the distance | AE | = 2, | DE | = 5 a | BE | = 4? - Railway embankment
 The railway embankment section is an isosceles trapezoid, and the bases' sizes are in the ratio of 5:3. The arms have a length of 5 m, and the embankment height is 4.8 m. Calculates the size of the embankment section area.
The railway embankment section is an isosceles trapezoid, and the bases' sizes are in the ratio of 5:3. The arms have a length of 5 m, and the embankment height is 4.8 m. Calculates the size of the embankment section area.
- Area and perimeter of rectangle
 The rectangle area is 3000 cm2, and one dimension is 10 cm larger than the other. Determine the perimeter of the rectangle.
The rectangle area is 3000 cm2, and one dimension is 10 cm larger than the other. Determine the perimeter of the rectangle. - Dimensions of the trapezoid
 One of the trapezoid bases is one-fifth larger than its height, and the second base is 1 cm larger than its height. Find the dimensions of the trapezoid if its area is 115 cm2
One of the trapezoid bases is one-fifth larger than its height, and the second base is 1 cm larger than its height. Find the dimensions of the trapezoid if its area is 115 cm2 - Equation of the circle
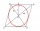 Find the equation of the circle inscribed in the rhombus ABCD where A[1, -2], B[8, -3], and C[9, 4].
Find the equation of the circle inscribed in the rhombus ABCD where A[1, -2], B[8, -3], and C[9, 4].
