Axial cut
The cone surface is 388.84 cm2, and the axial cut is an equilateral triangle. Find the cone volume.
Correct answer:

Tips for related online calculators
Do you want to convert length units?
Tip: Our volume units converter will help you convert volume units.
The Pythagorean theorem is the base for the right triangle calculator.
Calculation of an equilateral triangle.
See also our trigonometric triangle calculator.
Tip: Our volume units converter will help you convert volume units.
The Pythagorean theorem is the base for the right triangle calculator.
Calculation of an equilateral triangle.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
- algebra
- expression of a variable from the formula
- arithmetic
- square root
- solid geometry
- cone
- surface area
- planimetrics
- Pythagorean theorem
- area of a shape
- triangle
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Axial section
 Calculate the volume and surface of a cone whose axial section is an equilateral triangle with side length a = 18cm.
Calculate the volume and surface of a cone whose axial section is an equilateral triangle with side length a = 18cm. - Axial section
 The axial section of the cone is an equilateral triangle with an area 208 m². Calculate the volume of the cone.
The axial section of the cone is an equilateral triangle with an area 208 m². Calculate the volume of the cone. - Equilateral 73374
 The axial section of the cone is an equilateral triangle with a side of 12 cm. Surface and volume calculation.
The axial section of the cone is an equilateral triangle with a side of 12 cm. Surface and volume calculation. - Angle of cone
 The cone has a base diameter of 1.5 m. The angle at the central apex of the axial section is 86°. Calculate the volume of the cone.
The cone has a base diameter of 1.5 m. The angle at the central apex of the axial section is 86°. Calculate the volume of the cone. - Cone - from volume surface area
 The volume of the rotating cone is 1,018.87 dm3, and its height is 120 cm. What is the surface area of the cone?
The volume of the rotating cone is 1,018.87 dm3, and its height is 120 cm. What is the surface area of the cone? - Axial cut of a rectangle
 Calculate the volume and surface of the cylinder whose axial cut is a rectangle 15 cm wide with a diagonal of 25 cm long.
Calculate the volume and surface of the cylinder whose axial cut is a rectangle 15 cm wide with a diagonal of 25 cm long. - Axial section of the cone
 The axial section of the cone is an isosceles triangle in which the ratio of cone diameter to cone side is 2:3. Calculate its volume if you know its area is 314 cm square.
The axial section of the cone is an isosceles triangle in which the ratio of cone diameter to cone side is 2:3. Calculate its volume if you know its area is 314 cm square. - Cone side
 Calculate the volume and area of the cone whose height is 10 cm, and the axial section of the cone has an angle of 30 degrees between height and the cone side.
Calculate the volume and area of the cone whose height is 10 cm, and the axial section of the cone has an angle of 30 degrees between height and the cone side. - Rotary bodies
 The rotating cone and the rotary cylinder have the same volume of 180 cm³ and the same height, v = 15 cm. Which of these two bodies has a larger surface area?
The rotating cone and the rotary cylinder have the same volume of 180 cm³ and the same height, v = 15 cm. Which of these two bodies has a larger surface area? - 2x cone
 Circular cone height 84 cm was cut plane parallel with the base. The volume of these two small cones is the same. Calculate the height of the smaller cone.
Circular cone height 84 cm was cut plane parallel with the base. The volume of these two small cones is the same. Calculate the height of the smaller cone. - A spherical segment
 The aspherical section, whose axial section has an angle of j = 120° in the center of the sphere, is part of a sphere with a radius r = 10 cm. Calculate the cut surface.
The aspherical section, whose axial section has an angle of j = 120° in the center of the sphere, is part of a sphere with a radius r = 10 cm. Calculate the cut surface. - Cut and cone
 Calculate the volume of the rotation cone whose lateral surface is a circular arc with radius 15 cm and central angle 63 degrees.
Calculate the volume of the rotation cone whose lateral surface is a circular arc with radius 15 cm and central angle 63 degrees. - Surface area
 The volume of a cone is 1000 cm³, and the area of the axis cut is 100 cm². Calculate the surface area of the cone.
The volume of a cone is 1000 cm³, and the area of the axis cut is 100 cm². Calculate the surface area of the cone. - Cone - side
 Find the cone's surface area and volume if its height is 125 mm and the side length is 17 cm.
Find the cone's surface area and volume if its height is 125 mm and the side length is 17 cm. - Ratio of triangles areas
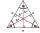 In an equilateral triangle ABC, the point T is its center of gravity, the point R is the image of the point T in axial symmetry along the line AB, and the point N is the image of the point T in axial symmetry along the line BC. Find the ratio of the areas
In an equilateral triangle ABC, the point T is its center of gravity, the point R is the image of the point T in axial symmetry along the line AB, and the point N is the image of the point T in axial symmetry along the line BC. Find the ratio of the areas - Consumption 4259
 What is the consumption of fabric per tent: Length 250, width 180, the height of triangle 120, sides 150 (all cm). What is the volume of air in the tent?
What is the consumption of fabric per tent: Length 250, width 180, the height of triangle 120, sides 150 (all cm). What is the volume of air in the tent? - Surface area and volume
 Find the surface area and volume of a rotating cone whose diameter is 60 mm and side length 3.4 cm.
Find the surface area and volume of a rotating cone whose diameter is 60 mm and side length 3.4 cm.
