Arc and segment
Calculate the length of circular arc l, area of the circular arc S1 and area of circular segment S2. The circle's radius is 11, and the corresponding angle is 122π.
Correct answer:
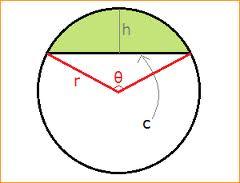
Tips for related online calculators
Most natural application of trigonometry and trigonometric functions is a calculation of the triangles. Common and less common calculations of different types of triangles offers our triangle calculator. Word trigonometry comes from Greek and literally means triangle calculation.
You need to know the following knowledge to solve this word math problem:
- algebra
- expression of a variable from the formula
- planimetrics
- circle
- area of a shape
- perimeter
- circular sector
- circular segment
- goniometry and trigonometry
- sine
Units of physical quantities:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Circle graph
 Erica surveyed students at her school about their favorite type of music. She made a circle graph to show the results. The central angle for the section of the graph that represents country music measures 72°. If 45 classmates chose the country as their f
Erica surveyed students at her school about their favorite type of music. She made a circle graph to show the results. The central angle for the section of the graph that represents country music measures 72°. If 45 classmates chose the country as their f - A goat 2
 As shown, a goat is tied at one corner of a rectangular shed by a 5-meter-long rope. The shed measures 3 m by 2 m and is surrounded by grassland. What is the area of the grassland in which the goat can graze? Give your answer to the nearest m².
As shown, a goat is tied at one corner of a rectangular shed by a 5-meter-long rope. The shed measures 3 m by 2 m and is surrounded by grassland. What is the area of the grassland in which the goat can graze? Give your answer to the nearest m². - Angle of the sector
 Find the angle of the sector of a circle radius of 20 units where the area is equal to the lateral area of a cone with a radius of 8 units.
Find the angle of the sector of a circle radius of 20 units where the area is equal to the lateral area of a cone with a radius of 8 units. - Lunes of Hippocrates
 Calculate the sum of the area of the so-called Hippocratic lunas, which were cut above the legs of a right triangle (a = 6cm, b = 8cm). Instructions: First, calculate the area of the semicircles above all sides of the ABC triangle. Compare the sum of the
Calculate the sum of the area of the so-called Hippocratic lunas, which were cut above the legs of a right triangle (a = 6cm, b = 8cm). Instructions: First, calculate the area of the semicircles above all sides of the ABC triangle. Compare the sum of the - Circular arc
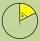 Calculate the center angle and length of the circular arc if the radius r = 21 cm and the area of the slice is 328.5 cm²
Calculate the center angle and length of the circular arc if the radius r = 21 cm and the area of the slice is 328.5 cm² - Circular segment
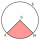 What is the radius of a circular section whose central angle is 36° and the area of S = 53.095 cm²?
What is the radius of a circular section whose central angle is 36° and the area of S = 53.095 cm²? - Goat
 The fenced flower bed has the shape of a regular hexagon. The tops are formed by fence posts. The fence around the flowerbed measures 60 m. A goat is tied to one of the pillars from the outside and grazes on the surrounding meadow (the goat should not ent
The fenced flower bed has the shape of a regular hexagon. The tops are formed by fence posts. The fence around the flowerbed measures 60 m. A goat is tied to one of the pillars from the outside and grazes on the surrounding meadow (the goat should not ent - A spherical segment
 The aspherical section, whose axial section has an angle of j = 120° in the center of the sphere, is part of a sphere with a radius r = 10 cm. Calculate the cut surface.
The aspherical section, whose axial section has an angle of j = 120° in the center of the sphere, is part of a sphere with a radius r = 10 cm. Calculate the cut surface. - Calculate 32321
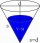 The shell of the cone is 62.8 cm². Calculate the side length and height of this cone if the diameter of the base is 8 cm.
The shell of the cone is 62.8 cm². Calculate the side length and height of this cone if the diameter of the base is 8 cm. - Surface of the cone
 Calculate the cone's surface if its height is 8 cm and the volume is 301.44 cm³.
Calculate the cone's surface if its height is 8 cm and the volume is 301.44 cm³. - Volume of the cone
 Calculate the cone's volume if its base area is 78.5 cm² and the shell area is 219.8 cm².
Calculate the cone's volume if its base area is 78.5 cm² and the shell area is 219.8 cm². - Sphere parts, segment
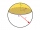 A sphere with a diameter of 20.6 cm, the cut is a circle with a diameter of 16.2 cm. What are the volume of the segment and the surface of the segment?
A sphere with a diameter of 20.6 cm, the cut is a circle with a diameter of 16.2 cm. What are the volume of the segment and the surface of the segment? - Flakes
 A circle was inscribed in the square. We draw a semicircle above each side of the square as above the diameter. This resulted in four chips. Which is bigger: the area of the middle square or the area of the four chips?
A circle was inscribed in the square. We draw a semicircle above each side of the square as above the diameter. This resulted in four chips. Which is bigger: the area of the middle square or the area of the four chips? - Spherical cap
 The spherical cap has a base radius of 8 cm and a height of 5 cm. Calculate the radius of a sphere of which this spherical cap is cut.
The spherical cap has a base radius of 8 cm and a height of 5 cm. Calculate the radius of a sphere of which this spherical cap is cut. - Circular 21273
 The dragon has the shape of a circular section with a central angle of 40 ° and a radius of 35 cm. How much paper do we need to make if 10% is added to the curved ones?
The dragon has the shape of a circular section with a central angle of 40 ° and a radius of 35 cm. How much paper do we need to make if 10% is added to the curved ones? - Mice
 Mice consumed a circular hole in a slice of cheese. The cheese is a circular cut with a radius of 20 cm and an angle of 90 degrees. What percentage of the cheese ate mice if they made 20 holes with a diameter of 2 cm?
Mice consumed a circular hole in a slice of cheese. The cheese is a circular cut with a radius of 20 cm and an angle of 90 degrees. What percentage of the cheese ate mice if they made 20 holes with a diameter of 2 cm? - Quarter circle
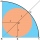 What is the radius of a circle inscribed in the quarter circle with a radius of 100 cm?
What is the radius of a circle inscribed in the quarter circle with a radius of 100 cm?
