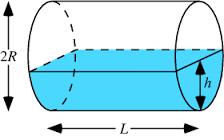
Horizontal Cylindrical Segment
How much fuel is in the horizontal cylindrical segment tank with a length of 10m, a width of level 1 meter, and a level is 0.2 meters below the tank's upper side?
Correct answer:
Tips for related online calculators
Tip: Our volume units converter will help you convert volume units.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Determine 82341
 Determine the equation of the circle that is the set of all points of the plane that are twice as far from the point [3,7] as they are from the point [0,1].
Determine the equation of the circle that is the set of all points of the plane that are twice as far from the point [3,7] as they are from the point [0,1]. - FGH right triangle
 Given a right triangle with leg lengths f and g, and hypotenuse h, if f = 7 cm and h = 11.2 cm, what is g?
Given a right triangle with leg lengths f and g, and hypotenuse h, if f = 7 cm and h = 11.2 cm, what is g? - A right 2
 A right triangle has legs with lengths of 24 cm and 21 cm if the length of the hypotenuse, in cm, can be written in the form of 3 sqrt(d), then what is the value of d?
A right triangle has legs with lengths of 24 cm and 21 cm if the length of the hypotenuse, in cm, can be written in the form of 3 sqrt(d), then what is the value of d? - General right triangle
 In a right triangle, if a =x+34 and b = x and c= 50, then solve for x. Side c is a hypotenuse. Then discuss the case when a or b is a hypotenuse.
In a right triangle, if a =x+34 and b = x and c= 50, then solve for x. Side c is a hypotenuse. Then discuss the case when a or b is a hypotenuse.
- RT area
 A right triangle has an area of 54cm². Calculate the sizes of both legs if the shorter leg is 75% of the size of the longer leg.
A right triangle has an area of 54cm². Calculate the sizes of both legs if the shorter leg is 75% of the size of the longer leg. - Angles in a triangle
 In a triangle, the first angle measures a number plus 45°, and the second angle is 30° less than the first angle. The third angle is two times the number more than the first angle. What are the measurements of each angle of the triangle?
In a triangle, the first angle measures a number plus 45°, and the second angle is 30° less than the first angle. The third angle is two times the number more than the first angle. What are the measurements of each angle of the triangle? - Find all
 Find all right-angled triangles whose side lengths form an arithmetic sequence.
Find all right-angled triangles whose side lengths form an arithmetic sequence. - A Pile of salt
 A Pile of salt has been stored in the shape of a cone. Mr. Terwilliker knows that the pile is 20 feet tall and 102 feet in circumference at the base. What area of the conical tarpaulin (a large sheet of material) is needed to cover the pile?
A Pile of salt has been stored in the shape of a cone. Mr. Terwilliker knows that the pile is 20 feet tall and 102 feet in circumference at the base. What area of the conical tarpaulin (a large sheet of material) is needed to cover the pile? - Sin cos tan
 If cos y = 0.8, 0° ≤ y ≤ 90°, find the value of (4 tan y) / (cos y-sin y)
If cos y = 0.8, 0° ≤ y ≤ 90°, find the value of (4 tan y) / (cos y-sin y)
- The radius
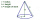 A right circular cone's radius and slant heights are 9 cm and 15 cm, respectively. Find, correct to one decimal place, the (i) Height (ii) Volume of the cone
A right circular cone's radius and slant heights are 9 cm and 15 cm, respectively. Find, correct to one decimal place, the (i) Height (ii) Volume of the cone - Isosceles right triangle
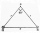 If the square of the hypotenuse of an isosceles right triangle is 128 cm2, find the length of each side.
If the square of the hypotenuse of an isosceles right triangle is 128 cm2, find the length of each side. - A construction
 A construction worker is trying to find the height of a skyrise building. He is standing some distance away from the base with an angle of elevation of 65 degrees. The worker moves 50 feet closer and measures the angle of elevation to be 75 degrees. Find
A construction worker is trying to find the height of a skyrise building. He is standing some distance away from the base with an angle of elevation of 65 degrees. The worker moves 50 feet closer and measures the angle of elevation to be 75 degrees. Find - A flagpole
 A flagpole is leaning at an angle of 107° with the ground. A string fastened to the top of the flagpole is holding up the pole. The string makes an angle of 38° with the ground, and the flagpole is 8 m long. What is the length of the string?
A flagpole is leaning at an angle of 107° with the ground. A string fastened to the top of the flagpole is holding up the pole. The string makes an angle of 38° with the ground, and the flagpole is 8 m long. What is the length of the string? - A hiker
 A hiker plans to hike up one side of a mountain and down the other side of points a mountain, each side of the mountain formed by a straight line. The angle of elevation at the starting point is 42.4 degrees, and the angle of elevation at the end is 48.3
A hiker plans to hike up one side of a mountain and down the other side of points a mountain, each side of the mountain formed by a straight line. The angle of elevation at the starting point is 42.4 degrees, and the angle of elevation at the end is 48.3
- Common chord
 The common chord of the two circles, c1 and c2, is 3.8 cm long. This chord forms an angle of 47° with the radius r1 in the circle c1. An angle of 24° 30' with the radius r2 is formed in the circle c2. Calculate both radii and the distance between the two
The common chord of the two circles, c1 and c2, is 3.8 cm long. This chord forms an angle of 47° with the radius r1 in the circle c1. An angle of 24° 30' with the radius r2 is formed in the circle c2. Calculate both radii and the distance between the two - Right triangle generator
 Detective Harry Thomson found on the Internet a generator of the lengths of the sides of right triangles according to which he must apply: a = 2xy, b = x² - y², c = x² + y², where are natural numbers and x & gt; y. Is it a working generator?
Detective Harry Thomson found on the Internet a generator of the lengths of the sides of right triangles according to which he must apply: a = 2xy, b = x² - y², c = x² + y², where are natural numbers and x & gt; y. Is it a working generator? - Radio radius
 Two friends have shortwave radios with a range of 13 km. The first of them travels by train at a speed of 48 km per hour along a straight section of track, from which the second of the friends is 5 km away. How long will radio friends be allowed for both
Two friends have shortwave radios with a range of 13 km. The first of them travels by train at a speed of 48 km per hour along a straight section of track, from which the second of the friends is 5 km away. How long will radio friends be allowed for both
