Hexagon rotation
A regular hexagon of side 6 cm is rotated at 60° along a line passing through its longest diagonal. What is the volume of the figure thus generated?
Correct answer:
Showing 2 comments:
Deepali.bhavale@gmail.com
Please specify the variables used ...using a figure will be great
Tips for related online calculators
Tip: Our volume units converter will help you convert volume units.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
- solid geometry
- cone
- cylinder
- pyramid
- planimetrics
- Pythagorean theorem
- right triangle
- circle
- polygon
- triangle
- diagonal
- basic functions
- reason
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Geometric Solid
 A concrete pipe is 1.0 m long. Its inside and outside diameters are 60 cm and 75 cm, respectively. What is the volume of the concrete (cubic meters) needed to make 25 pcs of pipe?
A concrete pipe is 1.0 m long. Its inside and outside diameters are 60 cm and 75 cm, respectively. What is the volume of the concrete (cubic meters) needed to make 25 pcs of pipe? - Wooden prism
 Find the weight of a regular wooden triangular prism with a height equal to the base's perimeter and a figure inscribed in a circle with a radius of 6.M cm, where M is the month of your birth. The density of oak is 680 kg/m³.
Find the weight of a regular wooden triangular prism with a height equal to the base's perimeter and a figure inscribed in a circle with a radius of 6.M cm, where M is the month of your birth. The density of oak is 680 kg/m³. - Radiators
 Calculate the radiator output if it has a thermal gradient (difference between inlet water and return temperatures) a) 5°C b) 10°C c) 15°C d) 20°C A heating water volume flow is 45 kg/h. How fast the water flows from the supply pipe to the radiator e) DN1
Calculate the radiator output if it has a thermal gradient (difference between inlet water and return temperatures) a) 5°C b) 10°C c) 15°C d) 20°C A heating water volume flow is 45 kg/h. How fast the water flows from the supply pipe to the radiator e) DN1 - Concentric circles 4
 One circle has a radius of 98 cm, and a second concentric circle has a 1m 26 cm radius. How much longer is the circumference of the second circle than that of the first?
One circle has a radius of 98 cm, and a second concentric circle has a 1m 26 cm radius. How much longer is the circumference of the second circle than that of the first? - ET inscribed circle
 An equilateral triangle has been inscribed in a circle with a radius of 4 cm . Find the area of the shaded region.
An equilateral triangle has been inscribed in a circle with a radius of 4 cm . Find the area of the shaded region. - Vertex of the rectangle
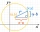 Determine the coordinates of the vertex of the rectangle inscribed in the circle x²+y² -2x-4y-20=0 if you know that one of its sides lies on the line p: x+2y=0
Determine the coordinates of the vertex of the rectangle inscribed in the circle x²+y² -2x-4y-20=0 if you know that one of its sides lies on the line p: x+2y=0 - Circle - analytics geometry
 Write the equation of the circle that passes through the points Q[3.5] R[2.6] and has its center on the line 2x+3y-4=0.
Write the equation of the circle that passes through the points Q[3.5] R[2.6] and has its center on the line 2x+3y-4=0. - Planetary system
 Robert has built a mechanical model solar system with three balls representing planets at the end of rods. Each rod is attached to the center, representing the Sun. The planets are lined up when he turns on the motor. The innermost planet makes a revoluti
Robert has built a mechanical model solar system with three balls representing planets at the end of rods. Each rod is attached to the center, representing the Sun. The planets are lined up when he turns on the motor. The innermost planet makes a revoluti - Determine 82341
 Determine the equation of the circle that is the set of all points of the plane that are twice as far from the point [3,7] as they are from the point [0,1].
Determine the equation of the circle that is the set of all points of the plane that are twice as far from the point [3,7] as they are from the point [0,1]. - Circular garden 2
 What is the area of the circular garden if the diameter of the circular garden is 4 meters?
What is the area of the circular garden if the diameter of the circular garden is 4 meters? - The minute
 The minute hand of a clock is 6 cm long. Find the area it sweeps between 2:05 PM and 2:40 PM.
The minute hand of a clock is 6 cm long. Find the area it sweeps between 2:05 PM and 2:40 PM. - The radius 2
 The radius of a circle is increased by 5%. What is the percentage increase in their circumference area?
The radius of a circle is increased by 5%. What is the percentage increase in their circumference area? - Understanding 81807
 The aquarium is 0.7m long and 25cm wide. The battery is deep if it can hold no more than 87.5 liters of water. I need help understanding how to calculate this.
The aquarium is 0.7m long and 25cm wide. The battery is deep if it can hold no more than 87.5 liters of water. I need help understanding how to calculate this. - Dimensions 81805
 The soap has the shape of a cuboid with dimensions of 6 cm, 4 cm, and 2 cm. Katy used it for a week and all the dimensions of the soap shrunk by half. How long will her soap last?
The soap has the shape of a cuboid with dimensions of 6 cm, 4 cm, and 2 cm. Katy used it for a week and all the dimensions of the soap shrunk by half. How long will her soap last? - Merly
 Merly prepared the table for lunch. She put a place mat that measures 5 dm long and 3 dm wide; she placed a plate on it with a diameter of 3 dm. How many mats can be seen on the table?
Merly prepared the table for lunch. She put a place mat that measures 5 dm long and 3 dm wide; she placed a plate on it with a diameter of 3 dm. How many mats can be seen on the table? - Garden hose
 Miguel wound a garden hose around a circular real. If the diameter of the real is 10 inches, how many inches of hose was wound on the first full turn of the real round? The answer to the nearest whole inch, use 3.14 for pi.
Miguel wound a garden hose around a circular real. If the diameter of the real is 10 inches, how many inches of hose was wound on the first full turn of the real round? The answer to the nearest whole inch, use 3.14 for pi. - The length 17
 The length of one of two chords of a circle is 12cm. If the chords are 6cm and 7cm, respectively, away from the center of the circle, calculate the length of the second chord.
The length of one of two chords of a circle is 12cm. If the chords are 6cm and 7cm, respectively, away from the center of the circle, calculate the length of the second chord.
