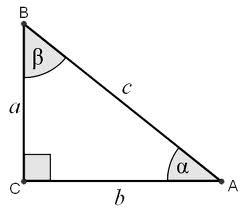
Right
Determine angles of the right triangle with the hypotenuse c and legs a, b, if: 3a+4b=4.9c
Correct answer:
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
- algebra
- quadratic equation
- planimetrics
- Pythagorean theorem
- right triangle
- triangle
- basic functions
- reason
- goniometry and trigonometry
- sine
- cosine
- tangent
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Hypotenuse and height
 In a right triangle is length of the hypotenuse c = 56 cm and height hc = 4 cm. Determine the length of both triangle legs.
In a right triangle is length of the hypotenuse c = 56 cm and height hc = 4 cm. Determine the length of both triangle legs. - RTriangle 17
 The hypotenuse of a right triangle is 17 cm. If you decrease both two legs by 3 cm, you will reduce the hypotenuse by 4 cm. Determine the length of these legs.
The hypotenuse of a right triangle is 17 cm. If you decrease both two legs by 3 cm, you will reduce the hypotenuse by 4 cm. Determine the length of these legs. - Area of RT
 The right triangle has orthogonal projections of legs to the hypotenuse lengths 15 cm and 9 cm. Determine the area of this triangle.
The right triangle has orthogonal projections of legs to the hypotenuse lengths 15 cm and 9 cm. Determine the area of this triangle. - RT a-b-x
 There is a right triangle with legs long a, b, and hypotenuse long x. Given that a = 6 cm and b = 9 cm, work out x. Give your answer as an exact surd.
There is a right triangle with legs long a, b, and hypotenuse long x. Given that a = 6 cm and b = 9 cm, work out x. Give your answer as an exact surd.
- Is right?
 Determine whether the triangle with legs (catheti) 19.5 cm and 26 cm and the length of the hypotenuse 32.5 cm is rectangular.
Determine whether the triangle with legs (catheti) 19.5 cm and 26 cm and the length of the hypotenuse 32.5 cm is rectangular. - RT sides
 Find the sides of a rectangular triangle if legs a + b = 17cm and the radius of the written circle ρ = 2cm.
Find the sides of a rectangular triangle if legs a + b = 17cm and the radius of the written circle ρ = 2cm. - Right triangle ABC
 Calculate the perimeter and area of a right triangle ABC. If you know the length of the legs, 4 cm, 5.5 cm, and 6.8 cm are the hypotenuse.
Calculate the perimeter and area of a right triangle ABC. If you know the length of the legs, 4 cm, 5.5 cm, and 6.8 cm are the hypotenuse. - General right triangle
 In a right triangle, if a =x+34 and b = x and c= 50, then solve for x. Side c is a hypotenuse. Then discuss the case when a or b is a hypotenuse.
In a right triangle, if a =x+34 and b = x and c= 50, then solve for x. Side c is a hypotenuse. Then discuss the case when a or b is a hypotenuse. - Right triangle Alef
 The obvod of a right triangle is 84 cm, and the hypotenuse is 37 cm long. Determine the lengths of the legs.
The obvod of a right triangle is 84 cm, and the hypotenuse is 37 cm long. Determine the lengths of the legs.
- Median in right triangle
 In the rectangular triangle, ABC has known the length of the legs a = 15cm and b = 36cm. Calculate the length of the median to side c (to hypotenuse).
In the rectangular triangle, ABC has known the length of the legs a = 15cm and b = 36cm. Calculate the length of the median to side c (to hypotenuse). - A right 2
 A right triangle has legs with lengths of 24 cm and 21 cm if the length of the hypotenuse, in cm, can be written in the form of 3 sqrt(d), then what is the value of d?
A right triangle has legs with lengths of 24 cm and 21 cm if the length of the hypotenuse, in cm, can be written in the form of 3 sqrt(d), then what is the value of d? - Right triangle - ratio
 The lengths of the legs of the right triangle ABC are in ratio b = 2:3. The hypotenuse is 10 cm long. Calculate the lengths of the legs of that triangle.
The lengths of the legs of the right triangle ABC are in ratio b = 2:3. The hypotenuse is 10 cm long. Calculate the lengths of the legs of that triangle. - Complementary angles 2
 Two complementary angles are (x+4) and (2x - 7). Find the value of x.
Two complementary angles are (x+4) and (2x - 7). Find the value of x. - Triangle 80994
 In the triangle, ABC, the angles alpha and beta axes subtend the angle phi = R + gamma/2. R is a right angle of 90°. Verify.
In the triangle, ABC, the angles alpha and beta axes subtend the angle phi = R + gamma/2. R is a right angle of 90°. Verify.
- Complete construction
 Construct triangle ABC if hypotenuse c = 7 cm and angle ABC = 30 degrees. / Use Thales' theorem - circle /. Measure and write down the length of the legs.
Construct triangle ABC if hypotenuse c = 7 cm and angle ABC = 30 degrees. / Use Thales' theorem - circle /. Measure and write down the length of the legs. - Hypotenuse 72524
 We know the height of the hypotenuse h = 4cm and the hypotenuse c = 19cm in a right triangle. How to calculate the segments of legs - sections on the hypotenuse c1, c2
We know the height of the hypotenuse h = 4cm and the hypotenuse c = 19cm in a right triangle. How to calculate the segments of legs - sections on the hypotenuse c1, c2 - Triangle 42
 Triangle BCA. Angles A=119° B=(3y+14) C=4y. What is the measure of triangle BCA=?
Triangle BCA. Angles A=119° B=(3y+14) C=4y. What is the measure of triangle BCA=?
