Hexagonal prism
The prism's base is a regular hexagon consisting of six triangles with side a = 12 cm and height va = 10.4 cm. The prism height is 5 cm. Find the volume and surface of the prism.
Correct answer:
Tips for related online calculators
See also our right triangle calculator.
Tip: Our volume units converter will help you convert volume units.
See also our trigonometric triangle calculator.
Tip: Our volume units converter will help you convert volume units.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
- solid geometry
- surface area
- prism
- planimetrics
- Pythagorean theorem
- right triangle
- polygon
- area of a shape
- perimeter
- triangle
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Building blocks
 Rosa bought a set of building blocks for her younger brother, Owen, for his birthday. Owen opened the gift and immediately used all 35 blocks in the set to build a tower shaped like a rectangular prism. Each block is a cube that is 1 1/2 inches along each
Rosa bought a set of building blocks for her younger brother, Owen, for his birthday. Owen opened the gift and immediately used all 35 blocks in the set to build a tower shaped like a rectangular prism. Each block is a cube that is 1 1/2 inches along each - A raft
 I want to build a raft, and I have beams with a square section with side a=20cm and length l=2m, wood density 670 kg/m³. I will connect 10 beams - what is the volume of the raft and its weight? How deep will a raft sink in water (water density 1000kg/m³)?
I want to build a raft, and I have beams with a square section with side a=20cm and length l=2m, wood density 670 kg/m³. I will connect 10 beams - what is the volume of the raft and its weight? How deep will a raft sink in water (water density 1000kg/m³)? - Dimensions 81957
 How many bricks are needed to build a wall that is 12 m long, 1.6 m high, and 47 cm wide if the dimensions of the brick are 30 x 15 x 7.5 cm and 5% of the wall volume is mortar?
How many bricks are needed to build a wall that is 12 m long, 1.6 m high, and 47 cm wide if the dimensions of the brick are 30 x 15 x 7.5 cm and 5% of the wall volume is mortar? - Understanding 81807
 The aquarium is 0.7m long and 25cm wide. The battery is deep if it can hold no more than 87.5 liters of water. I need help understanding how to calculate this.
The aquarium is 0.7m long and 25cm wide. The battery is deep if it can hold no more than 87.5 liters of water. I need help understanding how to calculate this. - The volume 8
 The volume of a right regular hexagonal prism is 187.2 cubic millimeters. The line segment that has a length of 2.6 millimeters begins at the center of the hexagon and ends at one side of the hexagon. 3 mm base. Find the height.
The volume of a right regular hexagonal prism is 187.2 cubic millimeters. The line segment that has a length of 2.6 millimeters begins at the center of the hexagon and ends at one side of the hexagon. 3 mm base. Find the height. - Water 66
 Water flows from a tap into a rectangular tank that measures 64cm by 36cm by 45cm. At 8 p. m., it is 1/4 filled with water. At 9 p. m., it is filled with 69,120 cm³ of water. Find the volume of water that has flowed into the tank from 8 p. m. to 9 p. m. G
Water flows from a tap into a rectangular tank that measures 64cm by 36cm by 45cm. At 8 p. m., it is 1/4 filled with water. At 9 p. m., it is filled with 69,120 cm³ of water. Find the volume of water that has flowed into the tank from 8 p. m. to 9 p. m. G - Cross-section 79984
 A ditch with a cross-section in the shape of an isosceles trapezoid with bases of 3 m and 5 m and arms of length 2 m is 2.5 meters deep and 10 meters long. How many cubic meters of soil did they have to excavate when digging it?
A ditch with a cross-section in the shape of an isosceles trapezoid with bases of 3 m and 5 m and arms of length 2 m is 2.5 meters deep and 10 meters long. How many cubic meters of soil did they have to excavate when digging it? - A cuboid 2
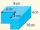 A cuboid with a depth of 4 cm but a length and width of x cm is cut out from one corner of the original cuboid as shown (the original cuboid has dimensions of 10x8x4 cm). The remaining shape has a volume of 199. Calculate the value of x.
A cuboid with a depth of 4 cm but a length and width of x cm is cut out from one corner of the original cuboid as shown (the original cuboid has dimensions of 10x8x4 cm). The remaining shape has a volume of 199. Calculate the value of x. - A rectangular 8
 A rectangular prism has a length of 10m, a height of 9m, and a width of 15m. What is its volume in cubic meters?
A rectangular prism has a length of 10m, a height of 9m, and a width of 15m. What is its volume in cubic meters? - Quadrilateral 70294
 The edge lengths of a quadrilateral prism are in the ratio a: b: c = 2:4:5. The surface of the prism is 57 cm². Calculate the volume.
The edge lengths of a quadrilateral prism are in the ratio a: b: c = 2:4:5. The surface of the prism is 57 cm². Calculate the volume. - Dimensions 69774
 Will a car with a load capacity of 3.5 t carry 50 oak planks and dimensions of 30 cm, 4 m, and 30 mm at a time?
Will a car with a load capacity of 3.5 t carry 50 oak planks and dimensions of 30 cm, 4 m, and 30 mm at a time? - Perimeter 64974
 The prism has a square base with an edge 5 cm long and 20 cm high. Calculate it: (a) the area of the base b) the perimeter of the base c) volume d) surface
The prism has a square base with an edge 5 cm long and 20 cm high. Calculate it: (a) the area of the base b) the perimeter of the base c) volume d) surface - Pool model
 The 1:500 scale pool model has internal dimensions of 15 cm, 10 cm, and 2.5 mm. Calculate how many hectoliters of water will be needed to fill a pool that will build according to this model.
The 1:500 scale pool model has internal dimensions of 15 cm, 10 cm, and 2.5 mm. Calculate how many hectoliters of water will be needed to fill a pool that will build according to this model. - Determine 5
 Determine the volume of an aquarium with these measurements: length = 78 cm ; width = 6 cm ; height = 43 cm using the formula V=lwh.
Determine the volume of an aquarium with these measurements: length = 78 cm ; width = 6 cm ; height = 43 cm using the formula V=lwh. - Prism - right isosceles
 Find the volume and surface of a prism with a height of 120 mm, the base of which is a right isosceles triangle with a leg length of 5 cm.
Find the volume and surface of a prism with a height of 120 mm, the base of which is a right isosceles triangle with a leg length of 5 cm. - The height of prism
 A right triangle forms the base of the vertical prism with perpendiculars 30 cm and 40 cm long. This prism has the same volume as a cube with an edge length of 3 dm. Find its height in cm.
A right triangle forms the base of the vertical prism with perpendiculars 30 cm and 40 cm long. This prism has the same volume as a cube with an edge length of 3 dm. Find its height in cm. - Wooden prism
 Find the weight of a regular wooden triangular prism with a height equal to the base's perimeter and a figure inscribed in a circle with a radius of 6.M cm, where M is the month of your birth. The density of oak is 680 kg/m³.
Find the weight of a regular wooden triangular prism with a height equal to the base's perimeter and a figure inscribed in a circle with a radius of 6.M cm, where M is the month of your birth. The density of oak is 680 kg/m³.
