Geometric seq
Find the third member of geometric progression if a1 + a2 = 36 and a1 + a3 = 90. Calculate its quotient.
Correct answer:
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Do you have a system of equations and looking for calculator system of linear equations?
Do you have a system of equations and looking for calculator system of linear equations?
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Determine 3938
 Determine the quotient and the first member of GP if a3 = 0.39, and a1 + a2 = 0.39.
Determine the quotient and the first member of GP if a3 = 0.39, and a1 + a2 = 0.39. - Determine 3948
 Determine the quotient and the first member of GP if a3 = 0.52, and a1 + a2 = 0.39.
Determine the quotient and the first member of GP if a3 = 0.52, and a1 + a2 = 0.39. - Sequence 5535
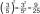 Find the value of the third member of the sequence if the sequence is given by: 3^n + 93.
Find the value of the third member of the sequence if the sequence is given by: 3^n + 93. - Determine 3755
 Find the third term and the quotient GP if a2 = -3, a1 + a2 = -2.5
Find the third term and the quotient GP if a2 = -3, a1 + a2 = -2.5
- Determine 3796
 Determine the quotient and the second GP member if a3 = -5, a2 + a3 = -7
Determine the quotient and the second GP member if a3 = -5, a2 + a3 = -7 - Quotient
 Determine the quotient and the second member of the geometric progression where a3=10, a1+a2=-1.6, and a1-a2=2.4.
Determine the quotient and the second member of the geometric progression where a3=10, a1+a2=-1.6, and a1-a2=2.4. - Determine 3914
 Find the quotient and the sixth term of GP if a1 = 420, a1 + a2 = 630.
Find the quotient and the sixth term of GP if a1 = 420, a1 + a2 = 630. - Determine 3746
 Determine the third and fourth member of GP if q = -0.6 and a1 + a2 = -0.2
Determine the third and fourth member of GP if q = -0.6 and a1 + a2 = -0.2 - Q of GP
 Calculate the quotient of geometric progression if a1=5 and a1+a2=12.
Calculate the quotient of geometric progression if a1=5 and a1+a2=12.
- Geometric sequence 5
 About members of the geometric sequence, we know: 3 a5:a3 = 27:25 7 a3 +5 a7 = 1 : 564 Calculate a1 (first member) and q (common ratio or q-coefficient)
About members of the geometric sequence, we know: 3 a5:a3 = 27:25 7 a3 +5 a7 = 1 : 564 Calculate a1 (first member) and q (common ratio or q-coefficient) - Determine 4053
 Determine the GP quotient if a1 = -0.8 and a1 + a2 = 0.64.
Determine the GP quotient if a1 = -0.8 and a1 + a2 = 0.64. - Calculate 3339
 A1 + a3 = 15 a1 + a2 + a3 = 21 Calculate a1 and q (quotient of the geometric sequence).
A1 + a3 = 15 a1 + a2 + a3 = 21 Calculate a1 and q (quotient of the geometric sequence). - Determine 4181
 Determine the fourth GP member if q = 4 and a1 + a3 = 5.44
Determine the fourth GP member if q = 4 and a1 + a3 = 5.44 - Geometric sequence
 In the geometric sequence is a4 = 20 a9 = -160. Calculate the first member a1 and quotient q.
In the geometric sequence is a4 = 20 a9 = -160. Calculate the first member a1 and quotient q.
- Determine 3876
 Determine the second term and the quotient GP if a3 = 48.6 a1 + a2 = 6
Determine the second term and the quotient GP if a3 = 48.6 a1 + a2 = 6 - Sequence
 Calculate what member of the sequence specified by (5n-2+15) has value 20.
Calculate what member of the sequence specified by (5n-2+15) has value 20. - Arithmetic progression
 In some arithmetic progression applies: 5a2 + 7a5 = 90 s3 = 12 Find the first member a =? and difference d =.
In some arithmetic progression applies: 5a2 + 7a5 = 90 s3 = 12 Find the first member a =? and difference d =.
