Rhombus construction
Construct ABCD rhombus if its diagonal AC=9 cm and side AB = 6 cm. Inscribe a circle in it, touching all sides.
Correct answer:
Showing 2 comments:
Dr Math
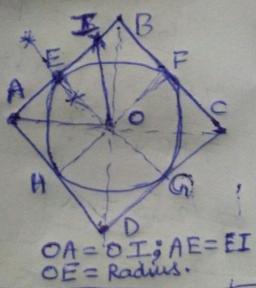
1. draw line segment AB = 6 cm
2. draw circle k1 (B, r=6 cm)
2. draw circle k2 (A, r=9 cm)
4. point C is intersect k1 and k2
5. draw line u2 from B perpendicular to AC
6. draw circle k3 (A, r=6 cm)
7. point D is intersect k3 and line u2
8. connect points ABCD to rhombus
9. point S is intersect of AC diagonal and BD diagonal
10. make perpendicular line u3 from S to AB.
11. draw inswribed circle with center S and radius SX, X is intersection of u3 and AB
2. draw circle k1 (B, r=6 cm)
2. draw circle k2 (A, r=9 cm)
4. point C is intersect k1 and k2
5. draw line u2 from B perpendicular to AC
6. draw circle k3 (A, r=6 cm)
7. point D is intersect k3 and line u2
8. connect points ABCD to rhombus
9. point S is intersect of AC diagonal and BD diagonal
10. make perpendicular line u3 from S to AB.
11. draw inswribed circle with center S and radius SX, X is intersection of u3 and AB
Dr Math
another steps:
1. Draw AC = 9cm horizontally.
2. With A as center and AB =6cm as radius, draw arcs above and below AC.
3. With C as center and AB as radius, draw arcs to cut the earlier arcs.
4. Intersection points are B and D.
5. Join all sides.
6. Draw BD. The intersection of AC AND BD is O , the center of the incircle.
7. Draw an arc with O as center and OB as radius to cut BC at E.
8. Draw perpendicular bisector of BE. It passes through O. Mid point of BE is F.
9. OF as radius and O as center draw the incircle.
1. Draw AC = 9cm horizontally.
2. With A as center and AB =6cm as radius, draw arcs above and below AC.
3. With C as center and AB as radius, draw arcs to cut the earlier arcs.
4. Intersection points are B and D.
5. Join all sides.
6. Draw BD. The intersection of AC AND BD is O , the center of the incircle.
7. Draw an arc with O as center and OB as radius to cut BC at E.
8. Draw perpendicular bisector of BE. It passes through O. Mid point of BE is F.
9. OF as radius and O as center draw the incircle.
You need to know the following knowledge to solve this word math problem:
Themes, topics:
Grade of the word problem:
Related math problems and questions:
- The marathon
 There are 12 athletes joining the Topolcany Marathon Event. How many ways can the first, second, and third placers be chosen?
There are 12 athletes joining the Topolcany Marathon Event. How many ways can the first, second, and third placers be chosen? - Richard
 Richard is conducting an experiment. Every time he flips a fair two-sided coin, he also rolls a six-sided die. What is the probability that the coin will land on tails and the die will land on an even number?
Richard is conducting an experiment. Every time he flips a fair two-sided coin, he also rolls a six-sided die. What is the probability that the coin will land on tails and the die will land on an even number? - Empty rooms
 In the tourist dormitory, 44 students slept in eight rooms, some of which were four-bed and others six-bed. When two beds were empty, how many four-bed and six-bed rooms were there in the dormitory?
In the tourist dormitory, 44 students slept in eight rooms, some of which were four-bed and others six-bed. When two beds were empty, how many four-bed and six-bed rooms were there in the dormitory? - One muffin
 Eight muffins and one drink cost $8.12. If the drink costs $1.24, find the cost of one muffin.
Eight muffins and one drink cost $8.12. If the drink costs $1.24, find the cost of one muffin.
- Mixed numbers equation
 4 5/9 is the same as the sum of 2 1/3 and 5/6 times a number. What is the number? Enter your answer as a mixed number in simplest form in the box.
4 5/9 is the same as the sum of 2 1/3 and 5/6 times a number. What is the number? Enter your answer as a mixed number in simplest form in the box. - A park on map
 A park has an area of ⅙ mi². On a map, the park has an area of 1 ¼ cm². On the map, how many square centimeters represent 1 mi²?
A park has an area of ⅙ mi². On a map, the park has an area of 1 ¼ cm². On the map, how many square centimeters represent 1 mi²? - The number 10
 The number of sides of two regular polygons differ by 1 the sum of the interior angles of the polygons is in the ratio of 3:2 calculate the number of sides of each polygon.
The number of sides of two regular polygons differ by 1 the sum of the interior angles of the polygons is in the ratio of 3:2 calculate the number of sides of each polygon. - Nautical vs statue mile
 A nautical mile is the unit of length used in sea and air navigation. A nautical mile is equal to 6,076 feet. What percent of a statue mile (5,280 ft) is a nautical mile?
A nautical mile is the unit of length used in sea and air navigation. A nautical mile is equal to 6,076 feet. What percent of a statue mile (5,280 ft) is a nautical mile? - Human population
 The populations of two cities after t years can be modeled by -150t+50,000 and 50t+75,000. What is the difference in the populations of the towns when t=4?
The populations of two cities after t years can be modeled by -150t+50,000 and 50t+75,000. What is the difference in the populations of the towns when t=4?
- The average 12
 The average of the first five numbers drawn was 2499. the first four numbers were 4165, 320, 7142, and 64. What was the fifth number?
The average of the first five numbers drawn was 2499. the first four numbers were 4165, 320, 7142, and 64. What was the fifth number? - Proportional relationship 3
 Which table below shows a proportional relationship? A. x ; y 3; 12 4; 16 5; 20 6; 24 7; 28 B. x ; y 3; 15 4; 20 5; 25 6; 35 7; 40 C. x ; y 3; 24 4; 32 5; 45 6; 48 7; 56 D. x ; y 3 ; 21 4; 24 5; 35 6; 42 7; 49
Which table below shows a proportional relationship? A. x ; y 3; 12 4; 16 5; 20 6; 24 7; 28 B. x ; y 3; 15 4; 20 5; 25 6; 35 7; 40 C. x ; y 3; 24 4; 32 5; 45 6; 48 7; 56 D. x ; y 3 ; 21 4; 24 5; 35 6; 42 7; 49 - Perimeter - general
 Solve: the perimeter of a triangle is 4x+1.if two of it side are(x+2) and (x-1). Find the third side.
Solve: the perimeter of a triangle is 4x+1.if two of it side are(x+2) and (x-1). Find the third side. - Families 83209
 Coal for 15 families lasts 60 days. How many days will the coal last for 20 families?
Coal for 15 families lasts 60 days. How many days will the coal last for 20 families? - The proportion
 The proportion's first, second, and third terms are 4, 20, and 13. Find the fourth term.
The proportion's first, second, and third terms are 4, 20, and 13. Find the fourth term.
- Farmer 8
 Farmer George cultivated 7/12 of his land with oranges and 1/5 of the remainder with cherries, and the remaining 40 acres he planted with cash crops. How much land did the farmer cultivate in all? What fraction of land does she plant with cherries?
Farmer George cultivated 7/12 of his land with oranges and 1/5 of the remainder with cherries, and the remaining 40 acres he planted with cash crops. How much land did the farmer cultivate in all? What fraction of land does she plant with cherries? - Charter flying service
 Henry and Wayne operate a charter flying service out of Breckenridge, which has an elevation of 9,600 feet above sea level. Henry has two flights scheduled for the day. He is taking a couple from Breckenridge to Hamilton, which has a 35% elevation drop. A
Henry and Wayne operate a charter flying service out of Breckenridge, which has an elevation of 9,600 feet above sea level. Henry has two flights scheduled for the day. He is taking a couple from Breckenridge to Hamilton, which has a 35% elevation drop. A - Isosceles 83157
 Using the cosine theorem, prove that in an isosceles triangle ABC with base AB, c=2a cos α.
Using the cosine theorem, prove that in an isosceles triangle ABC with base AB, c=2a cos α.
