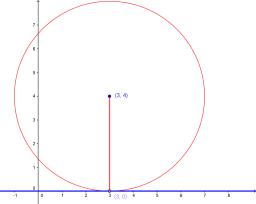
Equation of circle 2
Find the equation of a circle that touches the axis of y at a distance of 4 from the origin and cuts off an intercept of length 6 on the axis x.
Result
Result
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Circle
 Write the equation of a circle that passes through the point [0,6] and touches the X-axis point [5,0]: (x-x_S)²+(y-y_S)²=r²
Write the equation of a circle that passes through the point [0,6] and touches the X-axis point [5,0]: (x-x_S)²+(y-y_S)²=r² - Integer
 Find the integer whose distance on the numerical axis from number 1 is two times smaller than the distance from number 6.
Find the integer whose distance on the numerical axis from number 1 is two times smaller than the distance from number 6. - Equation of the circle
 Find the equation of the circle with the center at (1,20), which touches the line 8x+5y-19=0
Find the equation of the circle with the center at (1,20), which touches the line 8x+5y-19=0 - Equation of circle
 Find an equation of the circle with indicated properties: a. center at (-3,5), diameter 20. b. center at origin and diameter 16.
Find an equation of the circle with indicated properties: a. center at (-3,5), diameter 20. b. center at origin and diameter 16. - Sphere cuts
 At what distance from the center intersects the sphere with radius R = 91 plane if the cut area and area of the main sphere circle are in ratio 3/6?
At what distance from the center intersects the sphere with radius R = 91 plane if the cut area and area of the main sphere circle are in ratio 3/6? - Intercept with axis
 F(x)=log(x+4)-2, what is the x intercept
F(x)=log(x+4)-2, what is the x intercept - Coordinate 82855
 What is the ratio of the distance of the nearest and farthest point of the circle described by the equation x2+y2-16x-12y+75=0 from the origin of the coordinate system?
What is the ratio of the distance of the nearest and farthest point of the circle described by the equation x2+y2-16x-12y+75=0 from the origin of the coordinate system? - The frame
 Rodney has a board that is 5/6 yards long. He cuts 1/5 yard off the board and uses the rest of the board to make a frame. How much of the board is used to make the frame?
Rodney has a board that is 5/6 yards long. He cuts 1/5 yard off the board and uses the rest of the board to make a frame. How much of the board is used to make the frame? - Sphere in cone
 A sphere is inscribed in the cone (the intersection of their boundaries consists of a circle and one point). The ratio of the ball's surface and the area of the base is 4:3. A plane passing through the axis of a cone cuts the cone in an isosceles triangle
A sphere is inscribed in the cone (the intersection of their boundaries consists of a circle and one point). The ratio of the ball's surface and the area of the base is 4:3. A plane passing through the axis of a cone cuts the cone in an isosceles triangle - Circumference 7209
 The speed of the points lying on the circumference of the rotating disk is 6 m/s. The speed of the points, which lie 20 cm closer to the axis of rotation, is 4 m/s. Find the angular velocity of the wheel.
The speed of the points lying on the circumference of the rotating disk is 6 m/s. The speed of the points, which lie 20 cm closer to the axis of rotation, is 4 m/s. Find the angular velocity of the wheel. - A Piece 6
 A piece of material measures 40 inches. Sara cuts the material into two pieces, one measuring 14 inches. Write an addition equation that we could use to find the length of the other piece of the material.
A piece of material measures 40 inches. Sara cuts the material into two pieces, one measuring 14 inches. Write an addition equation that we could use to find the length of the other piece of the material. - A Cartesian framework
 1. In a Cartesian framework, the functions f and g we know that: The function (f) is defined by f (x) = 2x², the function (g) is defined by g (x) = x + 3, the point (O) is the origin of the reference, and point (C) is the point of intersection of the grap
1. In a Cartesian framework, the functions f and g we know that: The function (f) is defined by f (x) = 2x², the function (g) is defined by g (x) = x + 3, the point (O) is the origin of the reference, and point (C) is the point of intersection of the grap - A chord
 In a circle radius of 6 cm, a chord is drawn 3 cm from the center. Calculate the angle subtended by the cord at the center of the circle Hence find the length of the minor arc cut off by the chord.
In a circle radius of 6 cm, a chord is drawn 3 cm from the center. Calculate the angle subtended by the cord at the center of the circle Hence find the length of the minor arc cut off by the chord. - Touch x-axis
 Find the equations of circles that pass through points A (-2; 4) and B (0; 2) and touch the x-axis.
Find the equations of circles that pass through points A (-2; 4) and B (0; 2) and touch the x-axis. - Parametric equation
 Find the parametric equation of a line with y-intercept (0,-4) and a slope of -2.
Find the parametric equation of a line with y-intercept (0,-4) and a slope of -2. - Broken tree
 The tree is broken at 4 meters above the ground. The top of the tree touches the ground at a distance of 5 meters from the trunk. Calculate the original height of the tree.
The tree is broken at 4 meters above the ground. The top of the tree touches the ground at a distance of 5 meters from the trunk. Calculate the original height of the tree. - Function 3
 Function f(x)=a(x-r)(x-s) the graph of the function has x-intercept at (-4, 0) and (2, 0) and passes through the point (-2,-8). Find constant a, r, s.
Function f(x)=a(x-r)(x-s) the graph of the function has x-intercept at (-4, 0) and (2, 0) and passes through the point (-2,-8). Find constant a, r, s.
