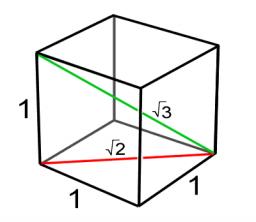
Body diagonal
Calculate the length of the body diagonal of the 6cm cube.
Correct answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Calculate 4694
 Calculate the length of the body diagonal in a cube of 15 cm.
Calculate the length of the body diagonal in a cube of 15 cm. - Diagonals 7084
 Calculate the lengths of the wall and body diagonals of the cube with an edge length of 10 cm.
Calculate the lengths of the wall and body diagonals of the cube with an edge length of 10 cm. - Calculate 64654
 Calculate the length of the wall and body diagonal in a cube with an edge of 60 cm.
Calculate the length of the wall and body diagonal in a cube with an edge of 60 cm. - Cube diagonals
 The cube has a wall area of 81 cm square. Calculate the length of its edge, wall, and body diagonal.
The cube has a wall area of 81 cm square. Calculate the length of its edge, wall, and body diagonal. - Body diagonal
 Find the cube surface if its body diagonal has a size of 6 cm.
Find the cube surface if its body diagonal has a size of 6 cm. - Calculate 24201
 Calculate the surface area, volume, and length of the body diagonal of a cube with an edge length of 4 dm.
Calculate the surface area, volume, and length of the body diagonal of a cube with an edge length of 4 dm. - Body diagonal - cube
 Calculate the surface and cube volume with a body diagonal 15 cm long.
Calculate the surface and cube volume with a body diagonal 15 cm long. - Calculate 83044
 The cube comprises 64 small cubes, each with an edge length of 15 mm. Calculate the wall length and body diagonals.
The cube comprises 64 small cubes, each with an edge length of 15 mm. Calculate the wall length and body diagonals. - Body diagonal
 Calculate the cube volume, whose body diagonal size is 75 dm. Draw a picture and highlight the body diagonally.
Calculate the cube volume, whose body diagonal size is 75 dm. Draw a picture and highlight the body diagonally. - Calculate 32133
 The cube has an area of 486 dm². Calculate the length of its side, its volume, the length of the body, and wall diagonals.
The cube has an area of 486 dm². Calculate the length of its side, its volume, the length of the body, and wall diagonals. - Measuring 65374
 Calculate the length of the body diagonal of a block measuring 6 cm, 7 cm, and 10 cm, and round the result to two decimal places.
Calculate the length of the body diagonal of a block measuring 6 cm, 7 cm, and 10 cm, and round the result to two decimal places. - Cube - angles
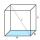 Calculate the angle between the wall diagonal and cube base. Calculate the angle between the cube body diagonal and the cube base.
Calculate the angle between the wall diagonal and cube base. Calculate the angle between the cube body diagonal and the cube base. - Decimetres 4163
 Determine the length of the body and wall diagonals of the cube, the volume of which is equal to 0.343 decimetres. Also, calculate its surface.
Determine the length of the body and wall diagonals of the cube, the volume of which is equal to 0.343 decimetres. Also, calculate its surface. - Angle of the body diagonals
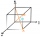 Using the vector dot product calculate the angle of the body diagonals of the cube.
Using the vector dot product calculate the angle of the body diagonals of the cube. - Dimensions 6264
 Calculate the length of the body diagonal of a block whose dimensions are a = 5cm, b = 6cm, c = 10cm.
Calculate the length of the body diagonal of a block whose dimensions are a = 5cm, b = 6cm, c = 10cm. - Diagonal 8192
 Find the volume and surface of a cube if you know the length of its body diagonal u = 216 cm.
Find the volume and surface of a cube if you know the length of its body diagonal u = 216 cm. - Cube diagonals
 Determine the volume and surface area of the cube if you know the length of the body diagonal u = 216 cm.
Determine the volume and surface area of the cube if you know the length of the body diagonal u = 216 cm.
