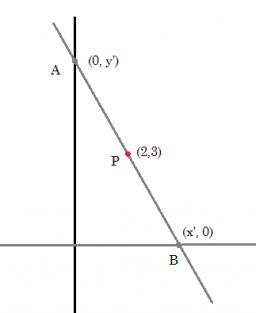
Coordinate axes

Determine the area of the triangle given by line -7x+7y+63=0 and coordinate axes x and y.

Result

S =  40.5

Solution:

Solution in text S =

Try another example






Leave us a comment of example and its solution (i.e. if it is still somewhat unclear...):

Showing 0 comments:
1st comment
Be the first to comment!
avatar




To solve this example are needed these knowledge from mathematics:

See also our right triangle calculator. Do you want to convert length units? See also our trigonometric triangle calculator. For Basic calculations in analytic geometry is helpful line slope calculator. From coordinates of two points in the plane it calculate slope, normal and parametric line equation(s), slope, directional angle, direction vector, the length of segment, intersections the coordinate axes etc.

Next similar examples:

  1. Vector - basic operations
    vectors_1 There are given points A [-9; -2] B [2; 16] C [16; -2] and D [12; 18] a. Determine the coordinates of the vectors u=AB v=CD s=DB b. Calculate the sum of the vectors u + v c. Calculate difference of vectors u-v d. Determine the coordinates of the vector w.
  2. Triangle IRT
    triangles_5 In isosceles right triangle ABC with right angle at vertex C is coordinates: A (-1, 2); C (-5, -2) Calculate the length of segment AB.
  3. Center
    triangle_axis Calculate the coordinates of the center of gravity T [x, y] of triangle ABC; A[11,4] B[13,-7] C[-17,-18].
  4. The farmer
    field_2 The farmer would like to first seed his small field. The required amount depends on the seed area. Field has a triangular shape. The farmer had fenced field, so he knows the lengths of the sides: 119, 111 and 90 meters. Find a suitable way to determine th
  5. Isosceles trapezoid
    lichobeznik Isosceles trapezoid ABCD, AB||CD is given by |CD| = c = 12 cm, height v = 16 cm and |CAB| = 20°. Calculate area of the trapezoid.
  6. Right isosceles
    right_isosceles_triangle Calculate area of the isosceles right triangle which perimeter is 49 cm.
  7. SAS triangle
    triangles2 The triangle has two sides long 7 and 19 and included angle 36°. Calculate area of this triangle.
  8. Sails
    ship_nina We known heights 220, 165 and 132 of sail. It has triangular shape. What is the surface of the sail?
  9. Triangle
    star Calculate the area of ​​the triangle ABC if b = c = 17 cm, R = 19 cm (R is the circumradius).
  10. Normal distribution GPA
    normal_d_3 The average GPA is 2.78 with a standard deviation of 4.5. What are students in the bottom the 20% having what GPA?
  11. Centre of mass
    centre_g_triangle The vertices of triangle ABC are from the line p distances 3 cm, 4 cm and 8 cm. Calculate distance from the center of gravity of the triangle to line p.
  12. Trapezium ABCD
    lichobeznik_5 In the figure, ABDC is a trapezium in which AB || CD. line segments RN and LM are drawn parallel to AB such that AJ=JK=KP. If AB=0.5m and AP=BQ=1.8m, find the lengths of AC, BD, RN and LM. angle D=angle C=60
  13. Cable car
    lanovka Cable car rises at an angle 45° and connects the upper and lower station with an altitude difference of 744 m. How long is "endless" tow rope?
  14. Vertices of RT
    RightTriangleMidpoint_3 Show that the points P1 (5,0), P2 (2,1) & P3 (4,7) are the vertices of a right triangle.
  15. Triangle P2
    1right_triangle Can triangle have two right angles?
  16. Theorem prove
    thales_1 We want to prove the sentense: If the natural number n is divisible by six, then n is divisible by three. From what assumption we started?
  17. Blocks
    cubes3_1 There are 9 interactive basic building blocks of an organization. How many two-blocks combinations are there?