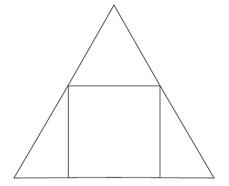
Equilateral triangle
A square is inscribed into an equilateral triangle with a side of 10 cm. Calculate the length of the square side.
Correct answer:
Tips for related online calculators
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
Calculation of an equilateral triangle.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Calculation of an equilateral triangle.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Calculate
 Calculate the length of a side of the equilateral triangle with an area of 50cm².
Calculate the length of a side of the equilateral triangle with an area of 50cm². - Equilateral 5140
 I have a circle with a diameter of 6.4 cm. I need to find out the length of the side of an equilateral triangle inscribed in a circle.
I have a circle with a diameter of 6.4 cm. I need to find out the length of the side of an equilateral triangle inscribed in a circle. - Circumference 4278
 An inscribed circle is also described as an equilateral triangle with a side length of 8 cm. How many cm is the circumference of the inscribed circle smaller than the circumference of the described circle?
An inscribed circle is also described as an equilateral triangle with a side length of 8 cm. How many cm is the circumference of the inscribed circle smaller than the circumference of the described circle? - Triangle eq
 Calculate accurate to hundredths cm height of an equilateral triangle with a side length 12 cm. Calculate also its perimeter and area.
Calculate accurate to hundredths cm height of an equilateral triangle with a side length 12 cm. Calculate also its perimeter and area. - Square circles
 Calculate the length of the described and inscribed circle to the square ABCD with a side of 5cm.
Calculate the length of the described and inscribed circle to the square ABCD with a side of 5cm. - Circle section
 An equilateral triangle with side 33 is an inscribed circle section whose center is in one of the triangle's vertices, and the arc touches the opposite side. Calculate: a) the length of the arc b) the ratio between the circumference to the circle sector a
An equilateral triangle with side 33 is an inscribed circle section whose center is in one of the triangle's vertices, and the arc touches the opposite side. Calculate: a) the length of the arc b) the ratio between the circumference to the circle sector a - Rhombus
 It is given a rhombus of side length a = 20 cm. Touchpoints of inscribed circle divided his sides into sections a1 = 13 cm and a2 = 7 cm. Calculate the radius r of the circle and the length of the diagonals of the rhombus.
It is given a rhombus of side length a = 20 cm. Touchpoints of inscribed circle divided his sides into sections a1 = 13 cm and a2 = 7 cm. Calculate the radius r of the circle and the length of the diagonals of the rhombus. - Square inscribed
 Find the length of the side of the square ABCD, which is inscribed to a circle k with a radius of 10 cm.
Find the length of the side of the square ABCD, which is inscribed to a circle k with a radius of 10 cm. - An equilateral
 An equilateral triangle is inscribed in a square of side 1 unit long so that it has one common vertex with the square. What is the area of the inscribed triangle?
An equilateral triangle is inscribed in a square of side 1 unit long so that it has one common vertex with the square. What is the area of the inscribed triangle? - Similarity coefficient
 The similarity ratio of two equilateral triangles is 4.3 (i.e., 43:10). The length of the side of the smaller triangle is 7.5 cm. Calculate the perimeter and area of the larger triangle.
The similarity ratio of two equilateral triangles is 4.3 (i.e., 43:10). The length of the side of the smaller triangle is 7.5 cm. Calculate the perimeter and area of the larger triangle. - Rhombus and inscribed circle
 It is given a rhombus with side a = 6 cm and the radius of the inscribed circle r = 2 cm. Calculate the length of its two diagonals.
It is given a rhombus with side a = 6 cm and the radius of the inscribed circle r = 2 cm. Calculate the length of its two diagonals. - Equilateral 81222
 A sphere is inscribed in an equilateral cone with a base diameter of 12 cm. Calculate the volume of both bodies. What percentage of the volume of the cone is filled by the inscribed sphere?
A sphere is inscribed in an equilateral cone with a base diameter of 12 cm. Calculate the volume of both bodies. What percentage of the volume of the cone is filled by the inscribed sphere? - Axial section
 Calculate the volume and surface of a cone whose axial section is an equilateral triangle with side length a = 18cm.
Calculate the volume and surface of a cone whose axial section is an equilateral triangle with side length a = 18cm. - ET inscribed circle
 An equilateral triangle has been inscribed in a circle with a radius of 4 cm . Find the area of the shaded region.
An equilateral triangle has been inscribed in a circle with a radius of 4 cm . Find the area of the shaded region. - Square and circle
 Into the square is an inscribed circle with a diameter of 10 cm. What is the difference between circumference square and circle?
Into the square is an inscribed circle with a diameter of 10 cm. What is the difference between circumference square and circle? - Height 2
 Calculate the height of the equilateral triangle with side 48.
Calculate the height of the equilateral triangle with side 48. - Prism - eq triangle
 Calculate the volume and surface of the prism with the base of an equilateral triangle with side a = 4cm, and the body height is 6cm.
Calculate the volume and surface of the prism with the base of an equilateral triangle with side a = 4cm, and the body height is 6cm.
