Evaluation of expressions
If a2-3a+1=0, find
(i)a2+1/a2
(ii) a3+1/a3
(i)a2+1/a2
(ii) a3+1/a3
Correct answer:
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
You need to know the following knowledge to solve this word math problem:
Grade of the word problem:
Related math problems and questions:
- Intersection of Q2 with line
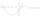 The equation of a curve C is y=2x² - 8x +9, and the equation of a line L is x + y=3. (1) Find the x-coordinates of the points of intersection of L and C. (ii) show that one of these points is also the
The equation of a curve C is y=2x² - 8x +9, and the equation of a line L is x + y=3. (1) Find the x-coordinates of the points of intersection of L and C. (ii) show that one of these points is also the - Zero fraction equation
 Find the value of y: 3/5y-9/4 (y +4) -1 = 1/2 (3y-2) -3 (3-y)
Find the value of y: 3/5y-9/4 (y +4) -1 = 1/2 (3y-2) -3 (3-y) - Three equations
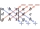 Find the solution to the equations x-y+z=-1 x+y+3z=-3 2x-y+2z=0
Find the solution to the equations x-y+z=-1 x+y+3z=-3 2x-y+2z=0 - Functions f,g
 Find g(1) if g(x) = 3x - x² Find f(5) if f(x) = x + 1/2
Find g(1) if g(x) = 3x - x² Find f(5) if f(x) = x + 1/2 - Fredrik
 Fredrik knows that x² + ax + b = 0 has only one solution, and this is x1 = - 3/2 Find the values of a and b.
Fredrik knows that x² + ax + b = 0 has only one solution, and this is x1 = - 3/2 Find the values of a and b. - Use L
 Use L Hospital's rule to solve (i) Lim x²+5x-14/x²-5x+6 X—>2 (ii)Lim x³+x²-x-1/x²-2x-3 X—>3
Use L Hospital's rule to solve (i) Lim x²+5x-14/x²-5x+6 X—>2 (ii)Lim x³+x²-x-1/x²-2x-3 X—>3 - Equation
 Find x: x + 1/2 = 1/3
Find x: x + 1/2 = 1/3 - Quadratic equation
 Find the roots of the quadratic equation: 3x²-4x + (-4) = 0.
Find the roots of the quadratic equation: 3x²-4x + (-4) = 0. - The product of the roots
 Find the product and the sum of the roots of x² + 3x - 9 = 0
Find the product and the sum of the roots of x² + 3x - 9 = 0 - Equation
 Solve equation with unknown x: 3 (1/3 + 2x) -2 (1/3-3x) -13/2 = 0
Solve equation with unknown x: 3 (1/3 + 2x) -2 (1/3-3x) -13/2 = 0 - Blank denominator
 1/4 + 5/blank =2/3 Find a blank number.
1/4 + 5/blank =2/3 Find a blank number. - Equation: 6200
 Solve the equation: 2y = 4 (0.5 + 3/2) -1
Solve the equation: 2y = 4 (0.5 + 3/2) -1 - Fractions and mixed numerals
 (a) Convert the following mixed numbers to improper fractions. i. 3 5/8 ii. 7 7/6 (b) Convert the following improper fraction to a mixed number. i. 13/4 ii. 78/5 (c) Simplify these fractions to their lowest terms. i. 36/42 ii. 27/45 (d) evaluate the follo
(a) Convert the following mixed numbers to improper fractions. i. 3 5/8 ii. 7 7/6 (b) Convert the following improper fraction to a mixed number. i. 13/4 ii. 78/5 (c) Simplify these fractions to their lowest terms. i. 36/42 ii. 27/45 (d) evaluate the follo - Expression 3143
 Determine the value of the expression 3x / 2 - 5/2 - 0,5x + 1 for x: a) x = 3 b) x = -3 c) x = 0
Determine the value of the expression 3x / 2 - 5/2 - 0,5x + 1 for x: a) x = 3 b) x = -3 c) x = 0 - Simple coefficient
 Find the value of k; if x = 3, y = 2 is a solution of the equation 2x + 3y = k.
Find the value of k; if x = 3, y = 2 is a solution of the equation 2x + 3y = k. - Missing number
 Blank +1/6 =3/2; find the missing number.
Blank +1/6 =3/2; find the missing number. - Equation 23
 Find the value of unknown x in the equation: x+3/x+1=5 (problem finding x)
Find the value of unknown x in the equation: x+3/x+1=5 (problem finding x)
