Bus vs train
Milada took the bus, and the journey took 55 minutes. Jarmila was 1h 20 min by train. They arrived in Prague at the same time, 10h45 min. At what time did each have to go out?
Result
Result
Tips for related online calculators
Need help calculating sum, simplifying, or multiplying fractions? Try our fraction calculator.
Do you want to convert time units like minutes to seconds?
Do you want to convert time units like minutes to seconds?
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Circle graph
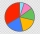 Erica surveyed students at her school about their favorite type of music. She made a circle graph to show the results. The central angle for the section of the graph that represents country music measures 72°. If 45 classmates chose the country as their f
Erica surveyed students at her school about their favorite type of music. She made a circle graph to show the results. The central angle for the section of the graph that represents country music measures 72°. If 45 classmates chose the country as their f - The angles 3
 The angles in a triangle are in the ratio of 3:4:5. Work out the size of each angle.
The angles in a triangle are in the ratio of 3:4:5. Work out the size of each angle. - Solve 13
 Solve the missing dimensions for the following triangle: Triangle ABC: AngleA=43 degrees, b=7.0cm, c=6.0cm Question 1. Angle B with units written as degrees Question 2. Angle C with units written as degrees Question 3. a, rounded to the nearest tenth of a
Solve the missing dimensions for the following triangle: Triangle ABC: AngleA=43 degrees, b=7.0cm, c=6.0cm Question 1. Angle B with units written as degrees Question 2. Angle C with units written as degrees Question 3. a, rounded to the nearest tenth of a - Sin cos tan
 If cos y = 0.8, 0° ≤ y ≤ 90°, find the value of (4 tan y) / (cos y-sin y)
If cos y = 0.8, 0° ≤ y ≤ 90°, find the value of (4 tan y) / (cos y-sin y) - The interior
 The interior angle of a regular polygon is x. If x is 9° less than the average of 153° and 145°, find the number of sides of the polygon.
The interior angle of a regular polygon is x. If x is 9° less than the average of 153° and 145°, find the number of sides of the polygon. - Regular polygons
 Two regular polygons, x and y, are such that the number of sides of x is three more than the number of the sides of y. If the sum of the exterior angles of x and y is 117°, how many sides have x?
Two regular polygons, x and y, are such that the number of sides of x is three more than the number of the sides of y. If the sum of the exterior angles of x and y is 117°, how many sides have x? - ABS, ARG, CONJ, RECIPROCAL
 Let z=-√2-√2i where i2 = -1. Find |z|, arg(z), z* (where * indicates the complex conjugate), and (1/z). Where appropriate, write your answers in the form a + i b, where both a and b are real numbers. Indicate the positions of z, z*, and (1/z) on an Argand
Let z=-√2-√2i where i2 = -1. Find |z|, arg(z), z* (where * indicates the complex conjugate), and (1/z). Where appropriate, write your answers in the form a + i b, where both a and b are real numbers. Indicate the positions of z, z*, and (1/z) on an Argand - A ship
 A ship has been spotted by two lighthouses, A and B, as shown in the figure. What is the distance from the ship to Lighthouse A to the nearest tenth? Figure - the distance between lighthouses A and B is 40 nautical miles. From A is seen in view angle 57°
A ship has been spotted by two lighthouses, A and B, as shown in the figure. What is the distance from the ship to Lighthouse A to the nearest tenth? Figure - the distance between lighthouses A and B is 40 nautical miles. From A is seen in view angle 57° - Triangle 75
 Triangle ABC has angle C bisected and intersected AB at D. Angle A measures 20 degrees, and angle B measures 40 degrees. The question is to determine AB-AC if length AD=1.
Triangle ABC has angle C bisected and intersected AB at D. Angle A measures 20 degrees, and angle B measures 40 degrees. The question is to determine AB-AC if length AD=1. - A construction
 A construction worker is trying to find the height of a skyrise building. He is standing some distance away from the base with an angle of elevation of 65 degrees. The worker moves 50 feet closer and measures the angle of elevation to be 75 degrees. Find
A construction worker is trying to find the height of a skyrise building. He is standing some distance away from the base with an angle of elevation of 65 degrees. The worker moves 50 feet closer and measures the angle of elevation to be 75 degrees. Find - Maggie
 Maggie observes a car and a tree from a window. The angle of depression of the car is 45 degrees, and that of the tree is 30 degrees. If the distance between the vehicle and the tree is 100 m, find Maggie's distance from the tree.
Maggie observes a car and a tree from a window. The angle of depression of the car is 45 degrees, and that of the tree is 30 degrees. If the distance between the vehicle and the tree is 100 m, find Maggie's distance from the tree. - Loonie
 Loonie has three wooden sticks measuring 17 inches, 21 inches, and 25 inches. He lays them down to form a triangle. Find the measure of the angle enclosed by 17 inches and 21 inches. (Express answers to the nearest hundredths) (using the law of cosines)
Loonie has three wooden sticks measuring 17 inches, 21 inches, and 25 inches. He lays them down to form a triangle. Find the measure of the angle enclosed by 17 inches and 21 inches. (Express answers to the nearest hundredths) (using the law of cosines) - An Elizabethan collar
 An Elizabethan collar is used to prevent an animal from irritating a wound. The angle between the opening (diameter 6 inches) with a 16-inch diameter and the side of the collar is 53 degrees. Find the surface area of the collar shown.
An Elizabethan collar is used to prevent an animal from irritating a wound. The angle between the opening (diameter 6 inches) with a 16-inch diameter and the side of the collar is 53 degrees. Find the surface area of the collar shown. - An angle of depression
 The lighthouse sees a ship at an angle of depression of 25°. The observer from the lighthouse is 82 m above sea level. How far is the ship from the top of the lighthouse?
The lighthouse sees a ship at an angle of depression of 25°. The observer from the lighthouse is 82 m above sea level. How far is the ship from the top of the lighthouse? - An isosceles
 An isosceles trapezoid has base angles of 50° each, and its bases are 20 cm and 30 cm. Compute its area.
An isosceles trapezoid has base angles of 50° each, and its bases are 20 cm and 30 cm. Compute its area. - At 5:00
 At 5:00 AM, the room temperature was 20°C. After six hours, the reading was 28°C. The temperature rose to how many degrees? What was the average change in temperature per hour?
At 5:00 AM, the room temperature was 20°C. After six hours, the reading was 28°C. The temperature rose to how many degrees? What was the average change in temperature per hour? - Deviation 70434
 Frustum has the base radii of the figures r1 and r2: r1> r2, r2 = s, and if the side deviation from the base plane is 60°. Express the surface and volume of the cone frustum using its side s.
Frustum has the base radii of the figures r1 and r2: r1> r2, r2 = s, and if the side deviation from the base plane is 60°. Express the surface and volume of the cone frustum using its side s.
