River
From the observatory 11 m high and 24 m from the riverbank, river width appears in the visual angle φ = 13°. Calculate the width of the river.
Correct answer:

Tips for related online calculators
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
Do you want to convert length units?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Do you want to convert length units?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
- algebra
- equation
- planimetrics
- Pythagorean theorem
- right triangle
- triangle
- The Law of Sines
- basic functions
- reason
- goniometry and trigonometry
- tangent
- arctangent
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Circle - analytics geometry
 Write the equation of the circle that passes through the points Q[3.5] R[2.6] and has its center on the line 2x+3y-4=0.
Write the equation of the circle that passes through the points Q[3.5] R[2.6] and has its center on the line 2x+3y-4=0. - Determine 82341
 Determine the equation of the circle that is the set of all points of the plane that are twice as far from the point [3,7] as they are from the point [0,1].
Determine the equation of the circle that is the set of all points of the plane that are twice as far from the point [3,7] as they are from the point [0,1]. - A student 5
 A student took the measurements of his classroom and gave the width as 7m and the length as 9m. If there is an error of 2 percent in measurement, determine the greatest value of [X+Y]/X if X and Y are the width and length of the classroom, respectively. G
A student took the measurements of his classroom and gave the width as 7m and the length as 9m. If there is an error of 2 percent in measurement, determine the greatest value of [X+Y]/X if X and Y are the width and length of the classroom, respectively. G - A piece 11
 A piece of wood is 220cm long. If 66cm is cut away from the wood, what percentage remains?
A piece of wood is 220cm long. If 66cm is cut away from the wood, what percentage remains?
- A lighthouse
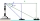 A lighthouse overlooks a bay, and it is 77 meters high. From the top, the lighthouse keeper can see a yacht southward at an angle of depression of 32 degrees and another boat eastward at an angle of 25 degrees. What is the distance between the boats?
A lighthouse overlooks a bay, and it is 77 meters high. From the top, the lighthouse keeper can see a yacht southward at an angle of depression of 32 degrees and another boat eastward at an angle of 25 degrees. What is the distance between the boats? - The length 17
 The length of one of two chords of a circle is 12cm. If the chords are 6cm and 7cm, respectively, away from the center of the circle, calculate the length of the second chord.
The length of one of two chords of a circle is 12cm. If the chords are 6cm and 7cm, respectively, away from the center of the circle, calculate the length of the second chord. - The factory 3
 The factory is 18 km away from the city. A cyclist leaves the factory for the city, and half an hour after him from the same place, a motorcyclist arrives 6 minutes before the cyclist in the city. Find the speed of each, knowing that the speed of the cycl
The factory is 18 km away from the city. A cyclist leaves the factory for the city, and half an hour after him from the same place, a motorcyclist arrives 6 minutes before the cyclist in the city. Find the speed of each, knowing that the speed of the cycl - The coordinates 3
 The coordinates of two vertices of an equilateral triangle are (1,1) and (5,1). What are the coordinates of the third vertex?
The coordinates of two vertices of an equilateral triangle are (1,1) and (5,1). What are the coordinates of the third vertex? - Cross-sectional 80979
 An undisciplined motorcyclist drove at an unreasonable speed on a mountain road, lost control in a bend, and left the roadway at 90 km/h. He was falling into a gully 36 m deep. Draw a cross-sectional picture of the whole situation. How far did the motorcy
An undisciplined motorcyclist drove at an unreasonable speed on a mountain road, lost control in a bend, and left the roadway at 90 km/h. He was falling into a gully 36 m deep. Draw a cross-sectional picture of the whole situation. How far did the motorcy
- Triangle 82
 Triangle PQR has vertices located at (2, 2), (5, -4), and (-4, -1). What type of triangle is triangle PQR?
Triangle PQR has vertices located at (2, 2), (5, -4), and (-4, -1). What type of triangle is triangle PQR? - Line segment
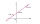 Find the length of the line joining points A(-4,8) and B(-1,4).
Find the length of the line joining points A(-4,8) and B(-1,4). - At week
 At week 3., the turtle was 5.45 centimeters long. At week 12, the turtle was 10.20 centimeters long. From week 12 to week 21, the turtle grew 0.5 centimeters less than it grew from week 3 to week 12. What was the length in centimeters of the turtle at wee
At week 3., the turtle was 5.45 centimeters long. At week 12, the turtle was 10.20 centimeters long. From week 12 to week 21, the turtle grew 0.5 centimeters less than it grew from week 3 to week 12. What was the length in centimeters of the turtle at wee - In the desert
 A man wondering in the desert walks 5.7 miles in the direction S 26° W. He then turns 90° and walks 9 miles in the direction N 49° W. At that time, how far is he from his starting point, and what is his bearing from his starting point?
A man wondering in the desert walks 5.7 miles in the direction S 26° W. He then turns 90° and walks 9 miles in the direction N 49° W. At that time, how far is he from his starting point, and what is his bearing from his starting point? - Number line
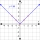 Find a number on the number line whose distance from the number 3 is four times smaller than from the number 15 (specify both solutions).
Find a number on the number line whose distance from the number 3 is four times smaller than from the number 15 (specify both solutions).
- Mountain climbing
 Ken and his brother decided to go on mountain climbing 8 miles from their house to Mt. Daraitan at a rate of x mph (miles per hour). For the return trip, it was 2 mph faster. It took them 6 hours for the entire round trip. What is the x?
Ken and his brother decided to go on mountain climbing 8 miles from their house to Mt. Daraitan at a rate of x mph (miles per hour). For the return trip, it was 2 mph faster. It took them 6 hours for the entire round trip. What is the x? - Equation of the circle
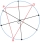 Find an equation of the circle whose diameter has endpoints (1,-4) and (3,2).
Find an equation of the circle whose diameter has endpoints (1,-4) and (3,2). - An archer
 An archer stands 60 meters (m) from a target. She launches an arrow that lands 3 centimeters (cm) from the bull's eye. The archer changes her position to 40 m from the target, and her next arrow lands 2 cm from the bull's eye. She changes her position to
An archer stands 60 meters (m) from a target. She launches an arrow that lands 3 centimeters (cm) from the bull's eye. The archer changes her position to 40 m from the target, and her next arrow lands 2 cm from the bull's eye. She changes her position to
