Right triangle from axes
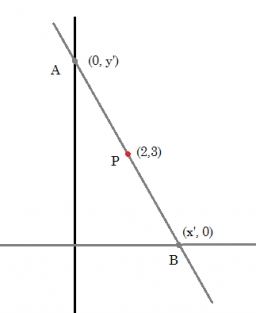
A line segment has its ends on the coordinate axes and forms a triangle of area equal to 36 square units. The segment passes through the point ( 5,2). What is the slope of the line segment?
Correct answer:
Tips for related online calculators
The line slope calculator is helpful for basic calculations in analytic geometry. The coordinates of two points in the plane calculate slope, normal and parametric line equation(s), slope, directional angle, direction vector, the length of the segment, intersections of the coordinate axes, etc.
Are you looking for help with calculating roots of a quadratic equation?
Need help calculating sum, simplifying, or multiplying fractions? Try our fraction calculator.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Are you looking for help with calculating roots of a quadratic equation?
Need help calculating sum, simplifying, or multiplying fractions? Try our fraction calculator.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
- geometry
- analytic geometry
- line
- line segment
- algebra
- quadratic equation
- expression of a variable from the formula
- planimetrics
- Pythagorean theorem
- right triangle
- area of a shape
- triangle
- numbers
- fractions
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Coordinate 82580
 Write the equation of the ellipse that passes through the points, and its axes are identical to the coordinate axes when A = [2, 3] and B = [−1, −4].
Write the equation of the ellipse that passes through the points, and its axes are identical to the coordinate axes when A = [2, 3] and B = [−1, −4]. - Direction vector
 The line p is given by the point P [- 0,5; 1] and the direction vector s = (1,5; - 3) determines: A) value of parameter t for points X [- 1,5; 3], Y [1; - 2] lines p B) whether the points R [0,5; - 1], S [1,5; 3] lies on the line p C) parametric equations
The line p is given by the point P [- 0,5; 1] and the direction vector s = (1,5; - 3) determines: A) value of parameter t for points X [- 1,5; 3], Y [1; - 2] lines p B) whether the points R [0,5; - 1], S [1,5; 3] lies on the line p C) parametric equations - Perpendicular 82994
 The straight line p is given by the formula y = 1/2 x - 1 . The line q is perpendicular to the line p and passes through the point A [1; 5]. Determine the y-coordinate of the point that intersects the line q with the y-axis.
The straight line p is given by the formula y = 1/2 x - 1 . The line q is perpendicular to the line p and passes through the point A [1; 5]. Determine the y-coordinate of the point that intersects the line q with the y-axis. - Line
 Line p passes through A[5, -3] and has a direction vector v=(2, 3). Is point B[3, -6] on the line p?
Line p passes through A[5, -3] and has a direction vector v=(2, 3). Is point B[3, -6] on the line p? - Slope of line
 What is the slope of the line that passes through the points: (-2, 4) and (-3, 1)?
What is the slope of the line that passes through the points: (-2, 4) and (-3, 1)? - A circle 2
 A circle is centered at the point (-7, -1) and passes through the point (8, 7). The radius of the circle is r units. The point (-15, y) lies in this circle. What are r and y (or y1, y2)?
A circle is centered at the point (-7, -1) and passes through the point (8, 7). The radius of the circle is r units. The point (-15, y) lies in this circle. What are r and y (or y1, y2)? - Circle - analytics geometry
 Write the equation of the circle that passes through the points Q[3.5] R[2.6] and has its center on the line 2x+3y-4=0.
Write the equation of the circle that passes through the points Q[3.5] R[2.6] and has its center on the line 2x+3y-4=0. - The slope 2
 What is the slope of the line that passes through the points (-4, -7) and (-2,-19)? Write your answer in the simplest form.
What is the slope of the line that passes through the points (-4, -7) and (-2,-19)? Write your answer in the simplest form. - Trapezoid MO-5-Z8
 ABCD is a trapezoid in that lime segment CE is divided into a triangle and parallelogram. Point F is the midpoint of CE, the DF line passes through the center of the segment BE, and the area of the triangle CDE is 3 cm². Determine the area of the trapezoi
ABCD is a trapezoid in that lime segment CE is divided into a triangle and parallelogram. Point F is the midpoint of CE, the DF line passes through the center of the segment BE, and the area of the triangle CDE is 3 cm². Determine the area of the trapezoi - Determine 82394
 Determine the equation of the circle that passes through the point M(-1,2) and N( 3,0) and whose center lies on the line p: x=-3+t, y=-1+t,
Determine the equation of the circle that passes through the point M(-1,2) and N( 3,0) and whose center lies on the line p: x=-3+t, y=-1+t, - Chord BC
 A circle k has the center at the point S = [0; 0]. Point A = [40; 30] lies on the circle k. How long is the chord BC if the center P of this chord has the coordinates [- 14; 0]?
A circle k has the center at the point S = [0; 0]. Point A = [40; 30] lies on the circle k. How long is the chord BC if the center P of this chord has the coordinates [- 14; 0]? - Sphere equation
 Obtain the equation of a sphere. Its center is on the line 3x+2z=0=4x-5y and passes through the points (0,-2,-4) and (2,-1,1).
Obtain the equation of a sphere. Its center is on the line 3x+2z=0=4x-5y and passes through the points (0,-2,-4) and (2,-1,1). - __________ 6734
 Draw a circle k (S, r = 2cm). Mark the three axes of symmetry of the circle defined by this circle. Each axis of symmetry of the circle passes through __________.
Draw a circle k (S, r = 2cm). Mark the three axes of symmetry of the circle defined by this circle. Each axis of symmetry of the circle passes through __________. - The slope
 Find the slope of the line that passes through the following two points: (-3, 16) and (-5, 30) Give your answer as a number, rounded to the nearest tenth, if necessary.
Find the slope of the line that passes through the following two points: (-3, 16) and (-5, 30) Give your answer as a number, rounded to the nearest tenth, if necessary. - Coordinate axes
 Find the triangle area given by line -7x+7y+63=0 and coordinate axes x and y.
Find the triangle area given by line -7x+7y+63=0 and coordinate axes x and y. - XY triangle
 Determine the area of a triangle given by line 7x+8y-69=0 and coordinate axes x and y.
Determine the area of a triangle given by line 7x+8y-69=0 and coordinate axes x and y. - KLMN trapezoid
 The KLMN trapezoid has bases KL 40cm and MN 16cm. On the KL base is point P. The segment NP divides the trapezoid into units with the same area. What is the distance of point P from point K?
The KLMN trapezoid has bases KL 40cm and MN 16cm. On the KL base is point P. The segment NP divides the trapezoid into units with the same area. What is the distance of point P from point K?
