Expressions 3
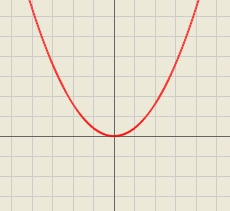
If k(x+6)= 4x2 + 20, what is k(10)=?
Correct answer:
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
You need to know the following knowledge to solve this word math problem:
Grade of the word problem:
Related math problems and questions:
- Geometric 20
 Find the geometric mean of 15 15 20 25 30.
Find the geometric mean of 15 15 20 25 30. - GEOMETRIC MEANS alternating
 Find the indicated number of geometric means between the pair of numbers. -32 and 4 [insert 2 means] Sequence:-32, _, _, 4
Find the indicated number of geometric means between the pair of numbers. -32 and 4 [insert 2 means] Sequence:-32, _, _, 4 - Book Store
 The Mabini Book Store (MBS) is reducing the prices of Mathematics books for promotion. The store has 6 Algebra books, 6 Geometry books, and 5 Statistics books to be arranged on a shelf. Books of the same kind are to be placed beside each other. How many w
The Mabini Book Store (MBS) is reducing the prices of Mathematics books for promotion. The store has 6 Algebra books, 6 Geometry books, and 5 Statistics books to be arranged on a shelf. Books of the same kind are to be placed beside each other. How many w - Two cables
 On a flat plain, two columns are erected vertically upwards. One is 7 m high, and the other 4 m. Cables are stretched between the top of one column and the foot of the other column. At what height will the cables cross? Assume that the cables do not sag.
On a flat plain, two columns are erected vertically upwards. One is 7 m high, and the other 4 m. Cables are stretched between the top of one column and the foot of the other column. At what height will the cables cross? Assume that the cables do not sag.
- Measurements: 44341
 Laboratory measurements determined the following roller lengths (in millimeters): {402; 410; 412; 410; 413; 418; 405; 409; 410; 409} Calculate arithmetic, geometric mean, mode, and median.
Laboratory measurements determined the following roller lengths (in millimeters): {402; 410; 412; 410; 413; 418; 405; 409; 410; 409} Calculate arithmetic, geometric mean, mode, and median. - Annual growth
 The population has grown from 25,000 to 33,600 in 10 years. Calculate what the average annual population growth in% was.
The population has grown from 25,000 to 33,600 in 10 years. Calculate what the average annual population growth in% was. - Statistics quiz
 Fill in the missing word. 1. in a data set, the mean, median and mode are measured of ________________ 2. "The manipulation of variables under controlled conditions"is the data collection method known as______________ 3. in a normal distribution, the area
Fill in the missing word. 1. in a data set, the mean, median and mode are measured of ________________ 2. "The manipulation of variables under controlled conditions"is the data collection method known as______________ 3. in a normal distribution, the area - Heptagonal pyramid
 A hardwood for a column is in the form of a frustum of a regular heptagonal pyramid. The lower base edge is 18 cm, and the upper base of 14 cm. The altitude is 30 cm. Determine the weight in kg if the wood density is 10 grams/cm³.
A hardwood for a column is in the form of a frustum of a regular heptagonal pyramid. The lower base edge is 18 cm, and the upper base of 14 cm. The altitude is 30 cm. Determine the weight in kg if the wood density is 10 grams/cm³. - Before yesterday
 The merchant adds a sale sign in his shop window to the shown pair of shoes in the morning: "Today by p% cheaper than yesterday. " After a while, however, he decided that the sign saying: "Today 62.5% cheaper than the day before yesterday". Determine the
The merchant adds a sale sign in his shop window to the shown pair of shoes in the morning: "Today by p% cheaper than yesterday. " After a while, however, he decided that the sign saying: "Today 62.5% cheaper than the day before yesterday". Determine the
- Frustum of a cone
 A reservoir contains 28.54 m³ of water when complete. The diameter of the upper base is 3.5 m, while the lower base is 2.5 m. Find the height if the reservoir is in the form of a frustum of a right circular cone.
A reservoir contains 28.54 m³ of water when complete. The diameter of the upper base is 3.5 m, while the lower base is 2.5 m. Find the height if the reservoir is in the form of a frustum of a right circular cone. - Profit growth
 A company's profit increased by 25% during 1992, increased by 40% during 1993, decreased by 20% in 1994, and increased by 10% during 1995. Find the average growth in the profit level over the four years periods.
A company's profit increased by 25% during 1992, increased by 40% during 1993, decreased by 20% in 1994, and increased by 10% during 1995. Find the average growth in the profit level over the four years periods. - Two cyclists 2
 At the same time, two cyclists left towns A and B at constant speeds. The first one goes from town A to town B, and the second one from town B to town A. At one point during the trip, they met. After they met, the first cyclist arrived at town B in 36min,
At the same time, two cyclists left towns A and B at constant speeds. The first one goes from town A to town B, and the second one from town B to town A. At one point during the trip, they met. After they met, the first cyclist arrived at town B in 36min, - Precious metals
 From 2006-2009, the value of precious metals changed rapidly. The data in the following table represent the total rate of return (in percentage) for platinum, gold, and silver from 2006 through 2009: Year Platinum Gold Silver 2009 62.7 25.0 56.8 2008 -41.
From 2006-2009, the value of precious metals changed rapidly. The data in the following table represent the total rate of return (in percentage) for platinum, gold, and silver from 2006 through 2009: Year Platinum Gold Silver 2009 62.7 25.0 56.8 2008 -41. - Coordinates of midpoint
 If the midpoint of the segment is (6,3) and the other end is (8,4), what is the coordinate of the other end?
If the midpoint of the segment is (6,3) and the other end is (8,4), what is the coordinate of the other end?
- Conical area
 A right-angled triangle has sides a=12 and b=19 at the right angle. The hypotenuse is c. If the triangle rotates on the c side as an axis, find the volume and surface area of the conical area created by this rotation.
A right-angled triangle has sides a=12 and b=19 at the right angle. The hypotenuse is c. If the triangle rotates on the c side as an axis, find the volume and surface area of the conical area created by this rotation. - Rectangle vs square
 One side of the rectangle is 1 cm shorter than the side of the square. The second side is 3 cm longer than the side of the square. The square and rectangle have the same area. Calculate the length of the sides of a square and a rectangle.
One side of the rectangle is 1 cm shorter than the side of the square. The second side is 3 cm longer than the side of the square. The square and rectangle have the same area. Calculate the length of the sides of a square and a rectangle. - Annual income
 The annual income (in thousands of $) of fifteen families is 60, 80, 90, 96, 120, 150, 200, 360, 480, 520, 1060, 1200, 1450, 2500, 7200. Calculate the harmonic and geometric mean.
The annual income (in thousands of $) of fifteen families is 60, 80, 90, 96, 120, 150, 200, 360, 480, 520, 1060, 1200, 1450, 2500, 7200. Calculate the harmonic and geometric mean.
