Sphere from tree points
Equation of sphere with three point (a,0,0), (0, a,0), (0,0, a) and center lies on plane x+y+z=a
Correct answer:

Showing 2 comments:
Dr Math
We found some bugs in this problem, but I think now is OK solution:
(x+a)2 + (y+a)2+(z-3a)2 = 6 a2
(x+a)2 + (y+a)2+(z-3a)2 = 6 a2
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Determine 82394
 Determine the equation of the circle that passes through the point M(-1,2) and N( 3,0) and whose center lies on the line p: x=-3+t, y=-1+t,
Determine the equation of the circle that passes through the point M(-1,2) and N( 3,0) and whose center lies on the line p: x=-3+t, y=-1+t, - Sphere equation
 Obtain the equation of a sphere. Its center is on the line 3x+2z=0=4x-5y and passes through the points (0,-2,-4) and (2,-1,1).
Obtain the equation of a sphere. Its center is on the line 3x+2z=0=4x-5y and passes through the points (0,-2,-4) and (2,-1,1). - Circle
 The circle touches two parallel lines, p, and q, and its center lies on line a, which is the secant of lines p and q. Write the equation of the circle and determine the coordinates of the center and radius. p: x-10 = 0 q: -x-19 = 0 a: 9x-4y+5 = 0
The circle touches two parallel lines, p, and q, and its center lies on line a, which is the secant of lines p and q. Write the equation of the circle and determine the coordinates of the center and radius. p: x-10 = 0 q: -x-19 = 0 a: 9x-4y+5 = 0 - X-coordinate 81737
 In triangle ABC, determine the coordinates of point B if you know that points A and B lie on the line 3x-y-5=0, points A and C lie on line 2x+3y+4=0, point C lies on the x-coordinate axis, and the angle at vertex C is right.
In triangle ABC, determine the coordinates of point B if you know that points A and B lie on the line 3x-y-5=0, points A and C lie on line 2x+3y+4=0, point C lies on the x-coordinate axis, and the angle at vertex C is right. - Chord BC
 A circle k has the center at the point S = [0; 0]. Point A = [40; 30] lies on the circle k. How long is the chord BC if the center P of this chord has the coordinates [- 14; 0]?
A circle k has the center at the point S = [0; 0]. Point A = [40; 30] lies on the circle k. How long is the chord BC if the center P of this chord has the coordinates [- 14; 0]? - Calculate 83160
 Calculate the distance of point A[ 4; 2; -3 ] from the plane : 2x - 2y + z + 5 = 0
Calculate the distance of point A[ 4; 2; -3 ] from the plane : 2x - 2y + z + 5 = 0 - Equation of the circle
 Find the equation of the circle with the center at (1,20), which touches the line 8x+5y-19=0
Find the equation of the circle with the center at (1,20), which touches the line 8x+5y-19=0 - Find parameters
 Find parameters of the circle in the plane - coordinates of center and radius: x²+(y-3)²=14
Find parameters of the circle in the plane - coordinates of center and radius: x²+(y-3)²=14 - Square ABCD
 Construct a square ABCD with center S [3,2] and the side a = 4 cm. Point A lies on the x-axis. Construct a square image in the displacement given by oriented segment SS'; S` [-1 - 4].
Construct a square ABCD with center S [3,2] and the side a = 4 cm. Point A lies on the x-axis. Construct a square image in the displacement given by oriented segment SS'; S` [-1 - 4]. - Lie/do not lie
 The rule f(x) = 8x+16 gives the function. Find whether point D[-1; 8] lies on this function. Solve graphically or numerically and give reasons for your answer.
The rule f(x) = 8x+16 gives the function. Find whether point D[-1; 8] lies on this function. Solve graphically or numerically and give reasons for your answer. - On line
 On line p: x = 4 + t, y = 3 + 2t, t is R, find point C, which has the same distance from points A [1,2] and B [-1,0].
On line p: x = 4 + t, y = 3 + 2t, t is R, find point C, which has the same distance from points A [1,2] and B [-1,0]. - Vertex of the rectangle
 Determine the coordinates of the vertex of the rectangle inscribed in the circle x²+y² -2x-4y-20=0 if you know that one of its sides lies on the line p: x+2y=0
Determine the coordinates of the vertex of the rectangle inscribed in the circle x²+y² -2x-4y-20=0 if you know that one of its sides lies on the line p: x+2y=0 - Sphere cuts
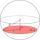 At what distance from the center intersects the sphere with radius R = 91 plane if the cut area and area of the main sphere circle are in ratio 3/6?
At what distance from the center intersects the sphere with radius R = 91 plane if the cut area and area of the main sphere circle are in ratio 3/6? - Calculate 8
 Calculate the coordinates of point B axially symmetrical with point A[-1, -3] along a straight line p : x + y - 2 = 0.
Calculate the coordinates of point B axially symmetrical with point A[-1, -3] along a straight line p : x + y - 2 = 0. - Centroid - two bodies
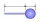 A body is composed of a 0.8 m long bar and a sphere with a radius of 0.1m attached so that its center lies on the longitudinal axis of the bar. Both bodies are of the same uniform material. The sphere is twice as heavy as the bar. Find the center of gravi
A body is composed of a 0.8 m long bar and a sphere with a radius of 0.1m attached so that its center lies on the longitudinal axis of the bar. Both bodies are of the same uniform material. The sphere is twice as heavy as the bar. Find the center of gravi - Perpendicular projection
 Determine the distance of a point B[1, -3] from the perpendicular projection of a point A[3, -2] on a straight line 2 x + y + 1 = 0.
Determine the distance of a point B[1, -3] from the perpendicular projection of a point A[3, -2] on a straight line 2 x + y + 1 = 0. - Circle
 From the equation of a circle: -x² -y² +16x -4y -59 = 0 Calculate the coordinates of the center of the circle S[x0, y0] and the radius of the circle r.
From the equation of a circle: -x² -y² +16x -4y -59 = 0 Calculate the coordinates of the center of the circle S[x0, y0] and the radius of the circle r.
