Pavement
Calculate the length of the pavement that runs through a circular square with a diameter of 40 m if the distance of the pavement from the center is 15 m.
Correct answer:

Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Circle chord
 What is the length x of the chord circle of diameter 115 m if the distance from the center circle is 11 m?
What is the length x of the chord circle of diameter 115 m if the distance from the center circle is 11 m? - Two parallel chords
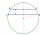 In a circle 70 cm in diameter, two parallel chords are drawn so that the circle's center lies between the chords. Calculate the distance of these chords if one of them is 42 cm long and the second 56 cm.
In a circle 70 cm in diameter, two parallel chords are drawn so that the circle's center lies between the chords. Calculate the distance of these chords if one of them is 42 cm long and the second 56 cm. - Calculate 80636
 Calculate the distance of a chord 19 cm long from the center of a circle with a diameter of 28 cm.
Calculate the distance of a chord 19 cm long from the center of a circle with a diameter of 28 cm. - Circle and square
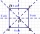 An ABCD square with a side length of 100 mm is given. Calculate the circle’s radius that passes through vertices B, C, and the center of the side AD.
An ABCD square with a side length of 100 mm is given. Calculate the circle’s radius that passes through vertices B, C, and the center of the side AD. - Circular 36163
 The circular park has an area of 31400 m². A trail runs across the center of the park. How long is it?
The circular park has an area of 31400 m². A trail runs across the center of the park. How long is it? - Cylinder-shaped 4411
 A cylinder-shaped hole with a diameter of 12 cm is drilled into a block of height 50 cm with a square base with an edge length of 20 cm. The axis of this opening passes through the center of the base of the cuboid. Calculate the volume and surface area of
A cylinder-shaped hole with a diameter of 12 cm is drilled into a block of height 50 cm with a square base with an edge length of 20 cm. The axis of this opening passes through the center of the base of the cuboid. Calculate the volume and surface area of - Circular arc
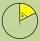 Calculate the center angle and length of the circular arc if the radius r = 21 cm and the area of the slice is 328.5 cm²
Calculate the center angle and length of the circular arc if the radius r = 21 cm and the area of the slice is 328.5 cm² - Tangents
 To circle with a radius of 41 cm from the point R guided two tangents. The distance of both points of contact is 16 cm. Calculate the distance from point R and circle center.
To circle with a radius of 41 cm from the point R guided two tangents. The distance of both points of contact is 16 cm. Calculate the distance from point R and circle center. - Circle chord
 Calculate the length of the chord of the circle with radius r = 10 cm, the length of which is equal to the distance from the circle's center.
Calculate the length of the chord of the circle with radius r = 10 cm, the length of which is equal to the distance from the circle's center. - The chord
 Calculate a chord length where the distance from the circle's center (S, 6 cm) equals 3 cm.
Calculate a chord length where the distance from the circle's center (S, 6 cm) equals 3 cm. - Touch circle
 Point A has a distance (A, k) = 10 cm from a circle k with radius r = 4 cm and center S. Calculate: a) the distance of point A from the point of contact T if the tangent to the circle is drawn from point A b) the distance of the contact point T from the l
Point A has a distance (A, k) = 10 cm from a circle k with radius r = 4 cm and center S. Calculate: a) the distance of point A from the point of contact T if the tangent to the circle is drawn from point A b) the distance of the contact point T from the l - Circular arc
 Calculate the length of the circular arc if the diameter d = 20cm and the angle alpha = 142 °
Calculate the length of the circular arc if the diameter d = 20cm and the angle alpha = 142 ° - Minute hand
 What is the distance the clock's minute hand travels in 12 minutes if the clock's diameter is 30 cm and the hand extends to a distance of 2 cm from the edge of the clock?
What is the distance the clock's minute hand travels in 12 minutes if the clock's diameter is 30 cm and the hand extends to a distance of 2 cm from the edge of the clock? - Calculate 32321
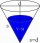 The shell of the cone is 62.8 cm². Calculate the side length and height of this cone if the diameter of the base is 8 cm.
The shell of the cone is 62.8 cm². Calculate the side length and height of this cone if the diameter of the base is 8 cm. - Chord BC
 A circle k has the center at the point S = [0; 0]. Point A = [40; 30] lies on the circle k. How long is the chord BC if the center P of this chord has the coordinates [- 14; 0]?
A circle k has the center at the point S = [0; 0]. Point A = [40; 30] lies on the circle k. How long is the chord BC if the center P of this chord has the coordinates [- 14; 0]? - The bridge
 A vehicle weighing 5,800 kg passes 41 km/h on an arched bridge with a radius of curvature of 62 m. What force pushes the car onto the bridge as it passes through the center? What maximum speed can it cross over the center of the bridge, so it does not fly
A vehicle weighing 5,800 kg passes 41 km/h on an arched bridge with a radius of curvature of 62 m. What force pushes the car onto the bridge as it passes through the center? What maximum speed can it cross over the center of the bridge, so it does not fly - Calculate 3561
 There is a 12 cm long chord in a circle with a radius of 10 cm. Calculate the distance of the chord from the center of the circle.
There is a 12 cm long chord in a circle with a radius of 10 cm. Calculate the distance of the chord from the center of the circle.
